
 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )| A. | 0.8πcm2 | B. | 3.2πcm2 | C. | 4πcm2 | D. | 4.8πcm2 |
分析 已知扇形底面半径是1cm,就可以知道展开图扇形的弧长是2πcm,根据弧长公式l=nπr÷180得到减去的圆心角的度数,然后根据扇形的面积公式计算.
解答 解:2π=$\frac{nπ×4}{180}$,解得:n=90°,
∵扇形彩纸片的圆心角是108°
∴剪去的扇形纸片的圆心角为108°-90°=18°.
剪去的扇形纸片的圆心角为18°.
减去的扇形纸片的面积为$\frac{18}{360}×π×{4}^{2}$=0.8πcm2,
故选A.
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 弧长确定,它所对的中心角和半径 | |
| B. | 长方形的长确定,它的周长与宽 | |
| C. | 扇形的中心角确定,它的面积与半径 | |
| D. | 正多边形边数确定,它的周长与边长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
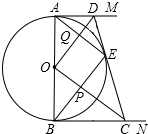 如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com