
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为![]() ,求直线MN的表达式(用含
,求直线MN的表达式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)在抛物线![]() 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(![]() ,
,![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
【答案】(1)不一定(2)直线MN的表达式为y=﹣x+m+n(3)抛物线的表达式为y=x2﹣2x﹣1
【解析】
试题分析:(1)设这一对“互换点”的坐标为(a,b)和(b,a).①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由![]() 可得
可得![]() ,于是得到结论;
,于是得到结论;
(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;
(3)设点A(p,q),则![]() ,由直线AB经过点P(
,由直线AB经过点P(![]() ,
,![]() ),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
试题解析:(1)不一定,
设这一对“互换点”的坐标为(a,b)和(b,a).
①当ab=0时,它们不可能在反比例函数的图象上,
②当ab≠0时,由![]() 可得
可得![]() ,即(a,b)和(b,a)都在反比例函数
,即(a,b)和(b,a)都在反比例函数![]() (k≠0)的图象上;
(k≠0)的图象上;
(2)由M(m,n)得N(n,m),设直线MN的表达式为y=cx+d(c≠0).
则有![]() 解得
解得![]() ,
,
∴直线MN的表达式为y=﹣x+m+n;
(3)设点A(p,q),则![]() ,
,
∵直线AB经过点P(![]() ,
,![]() ),由(2)得
),由(2)得![]() ,
,
∴p+q=1,
∴![]() ,
,
解并检验得:p=2或p=﹣1,
∴q=﹣1或q=2,
∴这一对“互换点”是(2,﹣1)和(﹣1,2),
将这一对“互换点”代入y=x2+bx+c得,
∴![]() 解得
解得![]() ,
,
∴此抛物线的表达式为y=x2﹣2x﹣1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】把一些书分给几名同学,若每人分11本,则有剩余,若( ),依题意,设有x名同学,可列不等式7(x+4)>11x.
A.每人分7本,则剩余4本
B.每人分7本,则剩余的书可多分给4个人
C.每人分4本,则剩余7本
D.其中一个人分7本,则其他同学每人可分4本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). 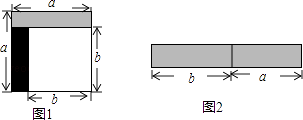
(1)上述操作能验证的等式是(填A或B)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
(2)应用你从(1)中选出的等式,计算: (1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )(1﹣
)(1﹣ ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com