
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 3 | 4 | 3 | … |
科目:初中数学 来源: 题型:解答题
| 时间第x(天) | 1≤x<30 | 30≤x≤50 |
| 售价(元/件) | x+30 | 60 |
| 每天销量(件) | 100-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
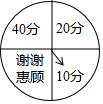 “五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com