解:(1)A、B两点的坐标分别为(0、5)、(5、0),
抛物线的解析式为y=-x
2+4x+5;
(2)①由题意知:P(5-t,0).
∴N(-(5-t)
2+4(5-t)+5,y)
∴MN=y
N-y
M=-(5-t)
2+4(5-t)+5-(-5+t+5)=-t
2+5t
∵以MN为直径的圆与y轴相切
∴-t
2+5t=2(5-t),

即t
2-7t+10=0,
解得t=2,t=5(不合题意舍去)
∴t的值为2;
②当CN∥DM时,CN=DM,
∵CN∥DM,直线AB的解析式为:y=-x+5
设直线CN的解析式为y=-x+h,易知:C(2,9).
∴直线CN的解析式为y=-x+11.
联立抛物线的解析式有:
-x+11=-x
2+4x+5,
解得x=2,x=3.
因此N点的横坐标为3,此时t=5-3=2.
根据抛物线的对称性可知:N点关于抛物线对称轴的对称点N′也应该符合条件,
因此N′的横坐标为1,此时t=5-1=4
∴t的值为2或4.
分析:(1)令直线的解析式中x=0,可求出B点坐标,令x=0,可求出A点坐标.然后将A、B的坐标代入抛物线中,即可求出抛物线的解析式.
(2)①以MN为直径的圆与y轴相切时,P点横坐标等于此时抛物线与直线AB函数值差的一半,据此来列等量关系求出P点的坐标,也就求出了t的值.
②如果CN∥AB,那么此时CN必与DM相等(因为此时四边形CDMN是平行四边形),可根据直线AB的斜率和C点坐标求出直线CN的解析式,联立抛物线的解析式可得出N点的坐标,根据抛物线的对称性和平行线分线段成比例定理可知,N点关于抛物线对称轴的对称点也应该符合这个条件,由此可求出两个符合条件的t的值.
点评:本题主要考查了二次函数解析式的确定以及函数图象交点等知识.

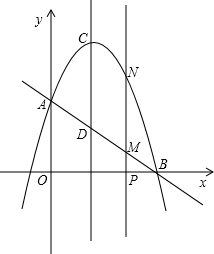 A、B两点.
A、B两点.


 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 如图,已知直线l1:y=
如图,已知直线l1:y=