练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知a、b是一元二次方程x2﹣2x﹣1=0的两个根，求a2﹣a+b+3ab的值．

    【答案】0

    【解析】试题分析：先由根与系数的关系得出a+b=2，ab=-1，将a2﹣a+b+3ab变形成含（a+2）和ab的形式.

    试题解析：

    ∵a、b是一元二次方程x2﹣2x﹣1=0的两个根

    ∴a+b=2，ab=-1； 且a2﹣2a﹣1=0

    即a2=2a+1 ；

    所以a2-a+b+3ab

    =2a+1-a+b3ab

    =a+b+1+3ab

    =2+1-3

    =0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(3z-y)2 等于（ ）

    A. 9z2-y+y2 B. 9z2-yz+y2 C. 9z2-6yz+y2 D. 3z2-6yz+y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O分别交AC，BM于点D，E.

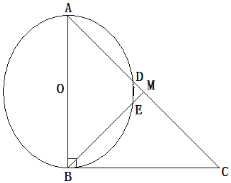
    （1）求证：MD=ME

    （2）填空：①若AB=6，当AD=2DM时，DE=___________；

    ②连接OD，OE，当∠A的度数为____________时，四边形ODME是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解实际问题

    华联商厦进货员在广州发现一种饰品，预计能畅销市场，就用8000元购进所有饰品，每件按58元很快卖完. 由于销路很好，又在上海用13200元购进，这次比在广州多进了100件，单价比广州贵了10%，但商厦仍按原售价销售，最后剩下的15件按八折销售，很快售完，问该商厦这两批饰品生意共赚了多少 ？(不考虑其它因素)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

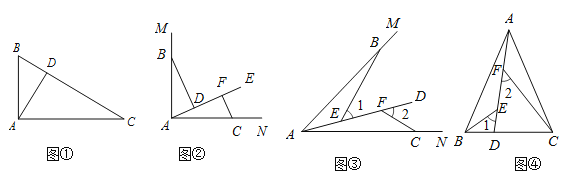
    【题目】问题情境：如图①，在直角三角形ABC中，∠BAC=，AD⊥BC于点D,可知：∠BAD=∠C（不需要证明）；

    （1）特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明：△ABD≌△CAF;

    （2）归纳证明：如图③，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证：△ABE≌△CAF;

    （3）拓展应用：如图④，在△ABC中，AB=AC，AB＞BC.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC.若△ABC的面积为15，则△ACF与△BDE的面积之和为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】⊙O的半径为5cm，圆心到弦AB的距离为3cm，则弦AB的长为______cm.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知2a－b＝3，则2b－4a＋3的值为(　　)

    A. －3 B. 9 C. －6 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.

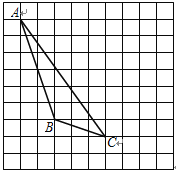
    （1）画出△ABC向右平移4个单位后得到的△A1B1C1；

    （2）图中AC与A1C1的关系是： _____________.

    （3）画出△ABC的AB边上的高CD；垂足是D；

    （4）图中△ABC的面积是_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列不等式变形中，错误的是(　　)

    A. 若 a≤b，则 a+c≤b+cB. 若 a+c≤b+c，则 a≤b

    C. 若 a≤b，则 ac2≤bc2D. 若 ac2≤bc2，则 a≤b

    查看答案和解析>>

    同步练习册答案