
分析 (1)根据关于x的一元二次方程x2-2x+3m-1=0有两个实数根分别为x1,x2,得出b2-4ac≥0,然后代入求解即可;
(2)根据根与系数的关系得出x1+x2=2,x1x2=3m-1,再把|x1-x2|=1进行变形,即可求出m的值;
(3)根据题意得出m=-x2+2x+1=-(x-1)2+2,再根据二次函数的性质即可得出答案.
解答 解:(1)∵x2-2x+3m-1=0有两个实数根分别为x1和x2,
∴b2-4ac=(-2)2-4(3m-1)≥0,
∴m≤$\frac{2}{3}$;
(2)∵x1+x2=2,x1x2=3m-1,
∴|x1-x2|2=|(x1+x2)2-4x1x2|=|4-4(3m-1)|=4|2-3m|=1,
∴2-3m=±$\frac{1}{4}$,
∴m=$\frac{7}{12}$或$\frac{3}{4}$(不合题意,舍去),
∴m=$\frac{7}{12}$;
(3)∵m=-x2+2x+1=-(x-1)2+2,
∴当x=1时,m有最大值,最大值是2.
点评 本题考查了根的判别式、根与系数的关系与二次函数的最值问题,一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
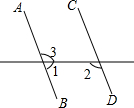 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )| A. | ∠2=70° | B. | ∠2=100° | C. | ∠2=110° | D. | ∠3=110° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com