
| 1 |
| 2 |
| ||
| 17 |
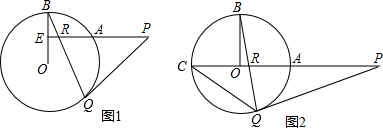
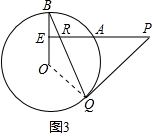 (1)证明:连接OQ,如图3,
(1)证明:连接OQ,如图3,| 1 |
| 2 |

| 1 |
| 2 |
| ||
| 17 |
| 17 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
| RH |
| BH |
| ||||
|
| 3 |
| 5 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
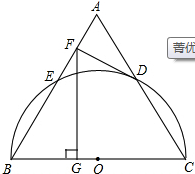 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
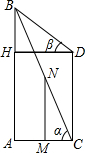 如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)
如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
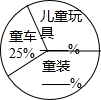 “六•一”快到了,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.图4是根据抽查结果绘制出的不完整的统计表和扇形图,请根据统计表和扇形图提供的信息,完成下列问题:
“六•一”快到了,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.图4是根据抽查结果绘制出的不完整的统计表和扇形图,请根据统计表和扇形图提供的信息,完成下列问题:| 类别 | 儿童玩具 | 童车 | 童装 |
| 抽查件数 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com