
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
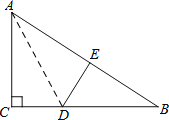
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】
试题分析:(1)根据折叠的性质得出∠C=∠AED=90°,利用∠DEB=∠C,∠B=∠B证明三角形相似即可;
(2)由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE,进而得出AD即可.
证明:(1)∵∠C=90°,△ACD沿AD折叠,
∴∠C=∠AED=90°,
∴∠DEB=∠C=90°,
又∵∠B=∠B,
∴△BDE∽△BAC;
(2)由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.
∴BE=AB﹣AE=10﹣6=4,
在Rt△BDE中,由勾股定理得,
DE2+BE2=BD2,
即CD2+42=(8﹣CD)2,
解得:CD=3,
在Rt△ACD中,由勾股定理得AC2+CD2=AD2,
即32+62=AD2,
解得:AD=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】去年2月“蒜你狠”风潮又一次来袭,某市蔬菜批发市场大蒜价格猛涨,原来单价4元/千克的大蒜,经过2月和3月连续两个月增长后,价格上升很快.物价部门紧急出台相关政策控制价格,4月大蒜价格下降了36%,恰好与涨价前的价格相同,则2月、3月的平均增长率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如下表
购票人数 | 1﹣50人 | 51﹣100人 | 100人以上 |
每人门票价 | 12元 | 10元 | 8元 |
某校八年(一)、(二)两班共100多人去游览该景点,其中(一)班不足50人,(二)班多于50人,如果两班都以班为单位分别购票,则一共付款1126元.如果以团体购票,则需要付费824元,问:
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
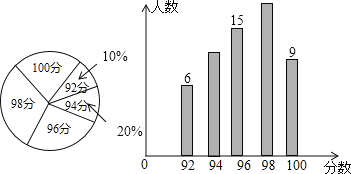
A.94分,96分 B.96分,96分 C.94分,96.4分 D.96分,96. 4分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.

(1)求证:AD平分∠BAC;
(2)求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com