
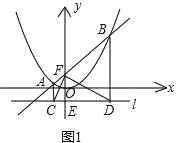
����Ŀ����֪����ͼ1������E��0��-1����ƽ����x���ֱ��l��������y=![]() x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
��1�����A��B��F�����ꣻ
��2����֤��CF��DF��
��3����P��������y=![]() x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ����OPQ����CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ����OPQ����CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A��-1��![]() ����B��4��4������F��0��1����2��֤������������3��P1��2��1����P2��8��16��
����B��4��4������F��0��1����2��֤������������3��P1��2��1����P2��8��16��
��������
�����������1������ϵ������⼴����
��2����Rt��CEF�������DEF�߳����ù��ɶ���֤��CF��DF��
��3������������⣬�ȼ�����ڣ����Ƿ��ҵ����������ĵ�P�����꣬����������������1��Rt��QPO��Rt��CFD����2��Rt��OPQ��Rt��CFD�����ݱ������P�����꣮
�����������1����ͼ1��
��x=-1ʱ��y=![]() ����x=4ʱ��y=4
����x=4ʱ��y=4
��A��-1��![]() ����B��4��4��
����B��4��4��
��ֱ��AB�Ľ���ʽΪy=kx+b
��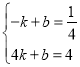 �����
�����![]()
��ֱ��AB�Ľ���ʽΪy=![]() x+1
x+1
��x=0ʱ��y=1
��F��0��1��
��2����Rt��CEF��CE=1��EF=2��
���ݹ��ɶ����ã�CF2=CE2+EF2=12+22=5��
��CF=![]()
��Rt��DEF��DE=4��EF=2
��DF2=DE2+EF2=42+22=20
��DF=2![]()
�ɣ�1����C��-1��-1����D��4��-1��
��CD=5
��CD2=52=25
��CF2+DF2=CD2
���CFD=90��
��CF��DF
��3�����ڣ���ͼ2��PM��x�ᣬ����Ϊ��M
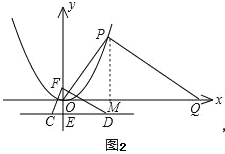
����PQ��OP
��Rt��OPM��Rt��OQP
��![]() ��
��![]()
��P��x��![]() x2����x��0����
x2����x��0����
��PM=![]() x2��OM=x
x2��OM=x
�ٵ�Rt��QPO��Rt��CFDʱ��![]()
��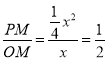
���x=2��P1��2��1��
�ڵ�Rt��OPQ��Rt��CFDʱ��![]()
��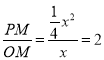
���x=8
��P2��8��16��
���ϣ����ڵ�P1��2��1����P2��8��16��ʹ����OPQ����CDF���ƣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�ս��������Ӳ����Ϸ����������ͬʱ����һöҼԪӲ�ң�
��1������Ϸ����Ϊ������öӲ����غ����泯��ʱ��С��Ӯ������С��Ӯ�����û���״ͼ���б��ķ�������С��Ӯ�ĸ��ʣ�
��2��С����Ϊ�������Ϸ����ƽ�����ǰѹ����Ϊ������öӲ�����涼����ʱ��С���8�֣�����С�յ�4�֣���ô���ĺ����Ϸ����ƽ����˵�����ɣ�������ƽ�����������������Ϸ����ʹ��Ϸ����ƽ������˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı��Ρ����Ρ����Ρ������ζ����е������ǣ� ��
A. �Խ�����ƽ��B. �Խ����ഹֱC. �Խ������D. �Խ����ഹֱƽ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����о�С��Ա�У���꼶ȫ��ͬѧ��������������е��飬���������鲿��ͬѧ�������Գɼ����ɸߵ��ͷ�A��B��C��D�ĸ��ȼ��������ݵ�������ݻ��Ƴ����µ�����ͳ��ͼ������ͳ��ͼ��
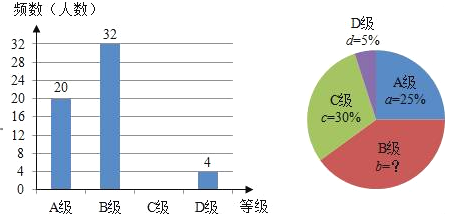
��������ϲ�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1���ÿ����о�С�鹲����� ��ͬѧ���������Գɼ�������ͳ��ͼ��B����ռ�İٷֱ�b= ��
��2����ȫ����ͳ��ͼ��
��3������У���꼶����400��ͬѧ������Ƹ�У���꼶ͬѧ�������Դ�꣨���Գɼ�C�����ϣ���C����Լ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У������˲���ȫ����鷽ʽ���ղ飩���ǣ���
A. ����������ѧ��ÿ��ѧϰ����ʱ��ĵ���
B. ��ȫ����ѧ������������״�ĵ���
C. ��ij��ѧ������6��5���������绷������֪������ĵ���
D. �������г���ѧ�������Ķ����ĵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ�����װ��120���졢��������ɫ��С����Щ�����ɫ��������ȫ��ͬ��ÿ������ǰ�Ƚ����������ҡ����������һ���������ɫ���ٷŻغ��ӣ�ͨ�������ظ�����������֣����������Ƶ���ȶ���0.3����ô���ƺ����к���ĸ���Ϊ�� ��
A. 36 B. 48 C. 70 D. 84
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��P��3��1��b������y��ĶԳƵ�Q�������ǣ�a����1������ab��ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com