
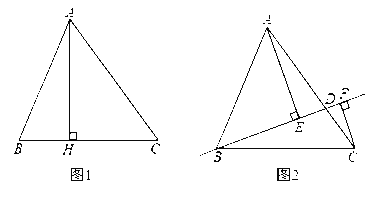
����Ŀ����ͼ1��2���ڡ�ABC�У�AB=13��BC=14��BH=5��
̽������ͼ1��AH��BC�ڵ�H����AH= ��AC= ����ABC�����![]() ��
��
��չ����ͼ2����D��AC�ϣ������A��C�غϣ����ֱ����A.C��ֱ��BD�Ĵ��ߣ�����ΪE��F����BD=x��AE=m��CF=n������D���A�غ�ʱ��������Ϊ![]() ��
��
��1���ú�x��m��n�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��
��2����m+n����x�ĺ�����ϵʽ������m+n�������ֵ����Сֵ��
��3���Ը�����һ��xֵ����ʱֻ��ȷ��Ψһ�ĵ�D��ֱ��д��������x��ȡֵ��Χ��
���𰸡�̽����12��15��84����չ��(1)![]() =
=![]() mx��
mx��![]() =
=![]() nx��(2)m+n=
nx��(2)m+n=![]() ��m+n�����ֵ15��m+n����СֵΪ12��(3) 11.2.
��m+n�����ֵ15��m+n����СֵΪ12��(3) 11.2.
�����������������̽�������ݹ��ɶ������㼴�ɣ�
��չ����1�����������ε������ʽ���㣻
��2��������ABC�������84���г���ϵʽ�������m+n����x�ĺ�����ϵʽ�����ͼ�������m+n�������ֵ����Сֵ��
��3�����ݵ�BD��ACʱ��m+n�����ֵ���
���������̽�����ɹ��ɶ����ã�AH=![]() =12��
=12��
AC=![]() =15��
=15��
��ABC�����S��ABC=![]() ��BC��AH=84.
��BC��AH=84.
�ʴ�Ϊ��12��15��84��
��չ����1��![]() =
=![]() ��BD��AE=
��BD��AE=![]() mx��
mx��
![]() =
=![]() ��BD��CH=
��BD��CH=![]() nx��
nx��
��2��![]() mx+
mx+![]() nx=84��
nx=84��
m+n=![]() ��
��
��BD��ACʱ��m+n�����ֵ15��
��BDֵ���ʱ��m+n����Сֵ��
������D���C�غ�ʱm+n����Сֵ��
��m+n����СֵΪ![]() =12��
=12��
��3����BD��ACʱ��
x=BD=![]() =11.2��ֻ��ȷ��Ψһ�ĵ�D��
=11.2��ֻ��ȷ��Ψһ�ĵ�D��


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ξ��ж�һ���ƽ���ı��β�һ�����е�������������
A.�Խ����
B.�Խ������
C.�Խ�����ƽ��
D.�Ա����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����β��߱��������ǣ� ��
A.�ı߶����B.�Խ���һ�����C.����Գ�ͼ��D.ÿһ���Խ���ƽ��һ��Խ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��9��AD��4. EΪCD����һ�㣬CE��6. ��P�ӵ�B��������ÿ��1����λ���ٶ����ű�BA���յ�A�˶�������PE�����P�˶���ʱ��Ϊt�룮
����AE�ij���
�Ƶ�tΪ��ֵʱ����PAEΪֱ�������Σ�
���Ƿ����������t��ʹEAǡ��ƽ�֡�PED�������ڣ����t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ�İ뾶����10���ף�ֱ�ߺ�Բֻ��һ�������㣬��Բ�ĵ�ֱ�ߵľ�����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��3����1������ô��P����x��ԳƵĵ�P��������ǣ� ��
A.����3��1��
B.��3��1��
C.����1��3��
D.����3����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=x2+bx+c�����㣨2��-3���ͣ�4��5��.
��1���������ߵı���ʽ���������ꣻ
��2������������x�ᷭ�ۣ��õ�ͼ��G����ͼ��G�ı���ʽ��
��3���ڣ�2���������£���-2<x<2ʱ��ֱ��y=m���ͼ����һ�������㣬��m��ֵ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�����������Ϊֱ�������εı߳����ǣ� ��
A.3��4��5
B.8��15��17
C.7��9��11
D.9��12��15
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com