
【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
【答案】(1)y=x-2x-3,顶点坐标为(1,-4).(2)y=-x+2x+3.(3)m的值为4,或-5<m≤3.
【解析】
试题分析:(1)把(2,-3)和(4,5)分别代入y=x+bx+c然后解方程组即可得到抛物线的表达式,配方化为顶点式可得顶点坐标;(2)利用对称性可得图象G的表达式;(3)y=m过抛物线顶点(1,4)时,直线y=m与该图象有一个公共点,此时y=4,∴m=4. 利用图象可确定另一情况-5<m≤3.
试题解析:(1)把(2,-3)和(4,5)分别代入y=x+bx+c
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的表达式为:y=x-2x-3.
∵y=x-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4).
(2)∵将抛物线沿x轴翻折,
得到图象G与原抛物线图形关于x轴对称,
∴图像G的表达式为:y=-x+2x+3.
(3)如图,

当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图象有一个公共点,
此时y=4,∴m=4.
当-2<x<0时,直线y=m与该图象有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3.


科目:初中数学 来源: 题型:
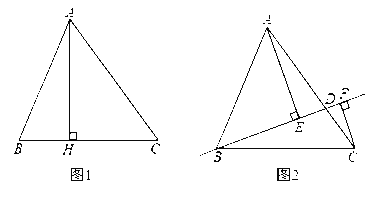
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质量检查员准备从一批产品中抽取10件进行检查,如果是随机抽取,为了保证每件产品被检的机会均等;
(1)请采用计算器模拟实验的方法,帮质量检查员抽取被检产品;
(2)如果没有计算器,你能用什么方法抽取被检产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直的四边形是菱形
D. 两条对角线互相垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子直径约为0.0000002cm,这个数量用科学记数法可表示为( )
A. 0.2×10-6cm B. 2×10-6cm C. 0.2×10-7cm D. 2×10-7cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com