练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x的方程x2﹣6x+k=0的两根分别是x1，x2，且满足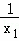+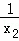=3，则k的值是　


    2　．解：∵3x2+2x﹣11=0的两个解分别为x1、x2，

    ∴x1+x2=6，x1x2=k，

    +===3，

    解得：k=2，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


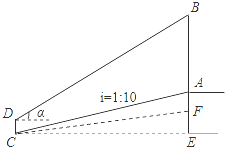
    数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度，如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α，已知tanα=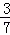，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：﹣（π﹣1）0﹣4sin45°；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


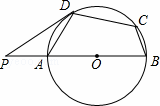
    如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

    　

    A．

    40°

    B．

    35°

    C．

    30°

    D．

    45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我市准备在相距2千米的M，N两工厂间修一条笔直的公路，但在M地北偏东45°方向、N地北偏西60°方向的P处，有一个半径为0.6千米的住宅小区（如图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据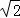：≈1.41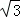，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


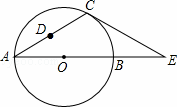
    如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．

    （1）试说明CE是⊙O的切线；

    （2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；

    （3）设点D是线段AC上任意一点（不含端点），连接OD，当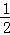CD+OD的最小值为6时，求⊙O的直径AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的方程x2+2x﹣m=0有两个相等的实数根，则m=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


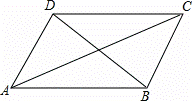
    小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（　　）

    　

    A．

    ①②

    B．

    ②③

    C．

    ①③

    D．

    ②④

    查看答案和解析>>

    同步练习册答案