
如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当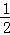 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
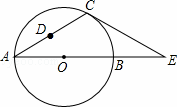
解:(1)连接OC,如图1,
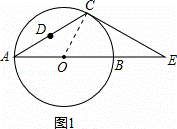
∵CA=CE,∠CAE=30°,
∴∠E=∠CAE=30°,∠COE=2∠A=60°,
∴∠OCE=90°,
∴CE是⊙O的切线;
(2)过点C作CH⊥AB于H,连接OC,如图2,
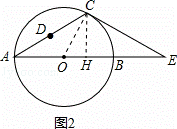
由题可得CH=h.
在Rt△OHC中,CH=OC•sin∠COH,
∴h=OC•sin60°=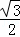 OC,
OC,
∴OC= =
=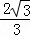 h,
h,
∴AB=2OC=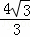 h;
h;
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,
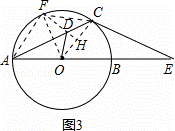
则∠AOF=∠COF=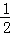 ∠AOC=
∠AOC=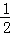 (180°﹣60°)=60°.
(180°﹣60°)=60°.
∵OA=OF=OC,
∴△AOF、△COF是等边三角形,
∴AF=AO=OC=FC,
∴四边形AOCF是菱形,
∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴DH=DC•sin∠DCH=DC•sin30°=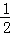 DC,
DC,
∴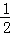 CD+OD=DH+F
CD+OD=DH+F D.
D.
根据两点之间线段最短可得:
当F、D、H三点共线时,DH+FD(即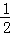 CD+OD)最小,
CD+OD)最小,
此时FH=OF•sin∠FOH=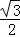 OF=6,
OF=6,
则OF=4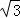 ,AB=2OF=8
,AB=2OF=8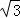 .
.
∴当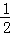 CD+OD的最小值为6时,⊙O的直径AB的长为8
CD+OD的最小值为6时,⊙O的直径AB的长为8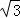 .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
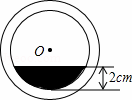
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
|
| A. | ( | B. | ( | C. | ( | D. | ( |
查看答案和解析>>
科目:初中数学 来源: 题型:
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 |
| 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com