
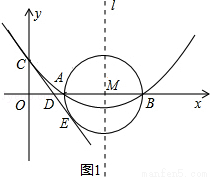
(12分)如图,已知抛物线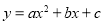 (
(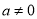 )的顶点坐标为(4,
)的顶点坐标为(4,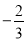 ),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
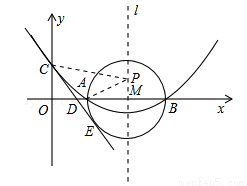
(1)求抛物线的解析式及A、B两点的坐标;
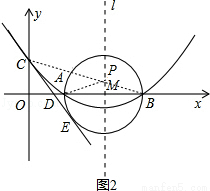
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小,若存在,求AP+CP的最小值;若不存在,请说明理由;
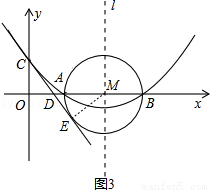
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
(1)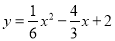 ,A(2,0)B(6,0);(2)存在,
,A(2,0)B(6,0);(2)存在,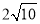 ;(3)
;(3)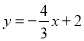 .
.
【解析】
试题分析:(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标;
(2)线段BC的长即为AP+CP的最小值;
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.
试题解析:(1)由题意,设抛物线的解析式为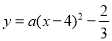 (
(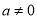 ),∵抛物线经过(0,2),∴
),∵抛物线经过(0,2),∴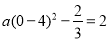 ,解得:
,解得: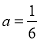 ,∴
,∴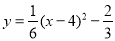 ,即:
,即: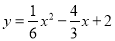 ,当
,当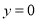 时,
时,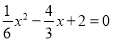 ,解得:
,解得: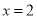 或
或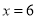 ,∴A(2,0),B(6,0);
,∴A(2,0),B(6,0);
(2)存在,如图2,由(1)知:抛物线的对称轴l为x=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小.∵B(6,0),C(0,2),∴OB=6,OC=2,∴BC=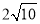 ,∴AP+CP=BC=
,∴AP+CP=BC=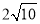 ,∴AP+CP的最小值为
,∴AP+CP的最小值为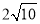 ;
;
(3)如图3,连接ME,∵CE是⊙M的切线,∴ME⊥CE,∠CEM=90°,∵C的坐标(0,2),∴OC=2,∵AB=4,∴ME=2,∴OC=ME=2,∵∠ODC=∠MDE,在△COD与△MED中,∵∠COD=∠MED,∠ODC=∠EDM,OC=ME,∴△COD≌△MED(AAS),∴OD=DE,DC=DM,设OD=x,则CD=DM=OM﹣OD=4﹣x,则Rt△COD中, 2,∴
2,∴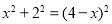 ,∴
,∴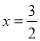 ,∴D(
,∴D(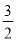 ,0),设直线CE的解析式为
,0),设直线CE的解析式为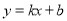 (
(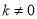 ),∵直线CE过C(0,2),D(
),∵直线CE过C(0,2),D(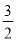 ,0)两点,则
,0)两点,则 ,解得:
,解得: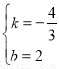 ,∴直线CE的解析式为
,∴直线CE的解析式为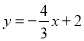 .
.
考点:二次函数综合题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:解答题
(本题满分13分)在平面直角坐标系 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.
),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.

(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E.
①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S,求S与t的函数关系式及S的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
如图,一个半径为r的圆形纸片在边长为 (
( )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
如图,点A、B、P为⊙O上的点,若∠PBO=15°,且PA∥OB,则∠AOB=( )
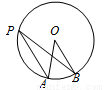
A.15° B.20° C.30° D.45°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:解答题
(8分)如图.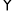 ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线
ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线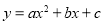 经过x轴上的点A、B.
经过x轴上的点A、B.
(1)求抛物线的解析式;
(2)写出x为何值时,函数值小于0.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:填空题
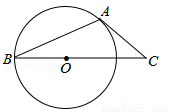
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25o,则∠C的大小等于______________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省伊春市九年级11月月考数学试卷(解析版) 题型:解答题
(8分)
如图所示,在平面直角坐标系中,抛物线 (
( )经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.

(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为( ,
, ),△PBE的面积为
),△PBE的面积为 ,求
,求 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com