
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.

【答案】(1)证明见解析;(2)点![]() 运动时间分别为
运动时间分别为![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)根据SAS证明即可;(2)分别讨论当AD=DQ,AD=AQ,AQ=DQ三种情况.
解:(1)在正方形ABCD中,AB=AD,∠DAC=∠BAC,
在△ADQ和△ABQ中,AD=AB,∠DAC=∠BAC,AQ=AQ,∴△ADQ≌△ABQ.
(2)①如图①中,当AQ=DQ时,∠QDA=∠QAD=45°,则点Q为正方形ABCD的中心,点B与点P重合,此时点P运动的时间为t1=4÷1=4(s);
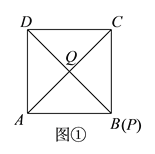
②图②中,当AQ=AD时,则∠ADQ=∠AQD,
∵正方形ABCD边长为4,∴AC![]() ,
,
∴CQ=AC-AQ=![]() ,
,
∵AD∥BC,∴∠CPQ=∠ADQ,
∴∠CPQ=∠AQD=∠CQP,∴CP=CQ=![]() ,
,
∴BP=![]() ,
,
∴P点运动的时间为t2=(4+8-![]() )÷1
)÷1![]() .
.
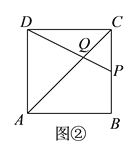
(3)如图③,当AD=DQ时,点C,P,Q三点重合,
此时P点运动时间为t3=(4+4)÷1=8(s).
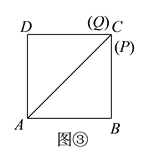
综上,当△ADQ恰为等腰三角形时,点P运动时间可以为4s, ![]() ,8s.
,8s.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形中,是因式分解的为( )
A. ab+ac+d=a(b+c)+dB. (x+2)(x﹣2)=x2﹣4
C. 6ab=2a3bD. x2﹣8x+16=(x﹣4)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
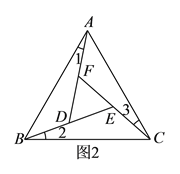
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com