
【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
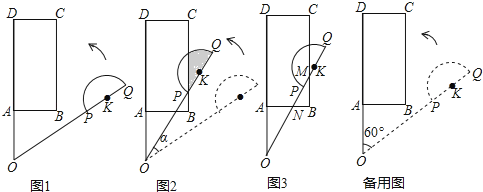
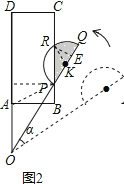
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
【答案】发现:α=30°,S阴影=![]() +
+![]() ;
;
拓展: BN=![]() ,0<x≤2
,0<x≤2![]() ﹣1;
﹣1;
探究: sinα的值为:![]() 或
或![]() 或
或![]()
【解析】
试题分析:首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,则可求得∠RKQ的度数,于是求得答案;
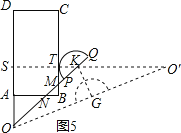
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN,即可求得BN,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF,则可求出x的取值范围;
探究:半圆K与矩形ABCD的边相切,分三种情况:①半圆K与BC相切于点T,②当半圆K与AD相切于T,③当半圆K与CD切线时,点Q与点D重合,且为切点;分别求解即可求得答案.
解:发现:如图2,设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,
过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°﹣30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ=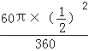 =
=![]() ,
,
在Rt△RKE中,RE=RKsin60°=![]() ,
,
∴S△PRK=![]() RE=
RE=![]() ,
,
∴S阴影=![]() +
+![]() ;
;
拓展:如图5,
∵∠OAN=∠MBN=90°,∠ANO=∠BNM,
∴△AON∽△BMN,
∴![]() ,即
,即![]() ,
,
∴BN=![]() ,
,
如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF=![]() ﹣AO=2
﹣AO=2![]() ﹣1,
﹣1,
∴x的取值范围是0<x≤2![]() ﹣1;
﹣1;
探究:半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,
则∠KSO=∠KTB=90°,
作KG⊥OO′于G,在Rt△OSK中,
OS=![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2![]() ,KO′=2
,KO′=2![]() ﹣
﹣![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG=![]() KO′=
KO′=![]() ﹣
﹣![]() ,
,
∴在Rt△OGK中,sinα=![]() =
=![]() =
=![]() ,
,
②当半圆K与AD相切于T,如图6,同理可得sinα=![]() =
=![]() =
=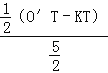 =
=![]() ;
;
③当半圆K与CD切线时,点Q与点D重合,且为切点,
∴α=60°,
∴sinα=sin60°=![]() ;
;
综上所述sinα的值为:![]() 或
或![]() 或
或![]() .
.
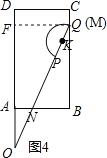


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某种品牌服装平均每天销售20件,每件盈利44元.销售过程中发现,在每件降价不超过10元的情况下,若每件降价1元,每天可多售5件.
(1)若每件降价2元,则每天售出 件,共盈利 元;
(2)如果销售这种品牌的服装每天要盈利2380元,求每件应降价多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
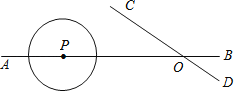
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=4cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒后⊙P与直线CD相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①倒数等于它本身的数有±1,
②绝对值等于它本身的数是正数,
③﹣ ![]() a2b3c是五次单项式,
a2b3c是五次单项式,
④2πr的系数是2,次数是2次,
⑤a2b2﹣2a+3是四次三项式,
⑥2ab2与3ba2是同类项.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.据此规律计算:每件商品降价元时,商场日盈利可达到2100元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快赣南的经济发展,鼓励农民创业.某农户承包荒山若干亩种植脐橙,投资59000元种植脐橙果树4000棵;今年脐橙总产量预测为60000千克,脐橙在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售2000千克,需4人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天300元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=2.5元,b=2元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)该农户加强果园管理,力争到明年纯收入达到84000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入﹣总支出)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com