
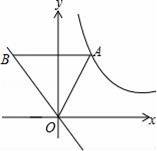
如图,点A为双曲线y=
 (x>0)的图象上一点,AB∥x轴交直线y=﹣x于点B.
(x>0)的图象上一点,AB∥x轴交直线y=﹣x于点B.
(1)若点B的纵坐标为2,比较线段AB和OB的大小关系;
(2)当点A在双曲线图象上运动时,代数式“AB2﹣OA2”的值会发生变化吗?请你作出判断,并说明理由.

【考点】反比例函数图象上点的坐标特征.
【分析】(1)根据题意求得A、B点的坐标,即可求得AB和OB的长,即可比较线段AB和OB的大小关系;
(2)设A(a,b),则B(﹣b,b),ab=2.所以利用两点间的距离公式可以求得线段AB、OA的长度;然后可以AB2﹣OA2的值.
【解答】解:(1)∵点B的纵坐标为2,AB∥x轴,
∴A(1,2),B(﹣2,2),
∴AB=3,OB=2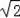
 ,
,
∴AB>OB;
(2)∵直线AB平行于x轴交直线y=
 于点A,
于点A,
故设A(a,b),
∵A为双曲线y=
 (x>0)上一点,
(x>0)上一点,
∴ab=2,
∵B纵坐标为b,
∴B(﹣b,b)
∴AB2﹣OA2=(a+b)2﹣[a2+b2]=2ab=4.
【点评】本题考查了反比例函数与一次函数图象上点的坐标特征,勾股定理的应用,利用点A的横坐标表示出点B的坐标是解题的关键.


科目:初中数学 来源: 题型:
如图,点O是矩形ABCD的边AD的中点,以O为圆心画
 ,一个动点P从O出发沿线段OA→线段AB→
,一个动点P从O出发沿线段OA→线段AB→
 →线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )
→线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )


A.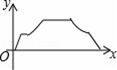
 B.
B.
 C.
C.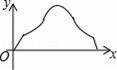
 D.
D.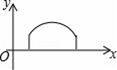

查看答案和解析>>
科目:初中数学 来源: 题型:
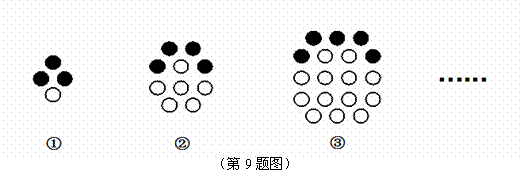
下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有1个空心小圆圈,第②个图形中一共有6个空心小圆圈,第③个图形中一共有13个空心小圆圈,…,按此规律排列,则第⑦个图形中空心小圆圈的个数为( ).
 |
A.61 B.63 C.76 D.78
查看答案和解析>>
科目:初中数学 来源: 题型:
在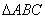 中,以
中,以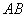 为斜边,作直角
为斜边,作直角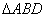 ,使点
,使点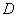 落在
落在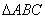 内,
内,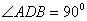 .
.
(1)如图1,若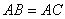 ,
,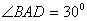 ,
,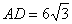 ,点
,点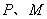 分别为
分别为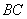 、
、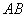 边的中点,连接
边的中点,连接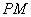 ,求线段
,求线段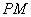 的长;
的长;
(2)如图2,若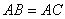 ,把
,把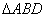 绕点
绕点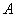 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到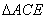 ,连接
,连接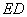 并延长交
并延长交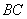 于点
于点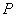 ,求证:
,求证: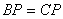 ;
;
(3)如图3,若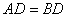 ,过点
,过点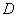 的直线交
的直线交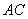 于点
于点 ,交
,交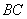 于点
于点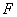 ,
,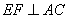 ,且
,且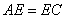 ,请直接写出线段
,请直接写出线段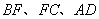 之间的关系(不需要证明).
之间的关系(不需要证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com