
如图,已知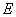 ,
,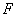 分别是正方形
分别是正方形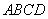 边
边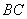 、
、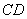 的中点,
的中点,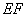 与
与 交于点
交于点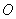 ,
,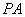 、
、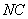 都垂直于平面
都垂直于平面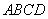 ,且
,且 ,
, ,
,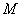 是线段
是线段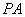 上一动
上一动 点.
点.
(Ⅰ)求证:平面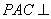 平面
平面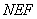 ;
;
(Ⅱ)若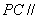 平面
平面 ,试求
,试求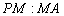 的值;
的值;
(Ⅲ)当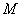 是
是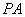 中点时,求二面角
中点时,求二面角 的余弦值.
的余弦值.

解:法1:(Ⅰ)连结 ,
,
∵ 平面
平面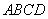 ,
, 平面
平面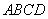 ,∴
,∴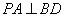 ,
,
 又∵
又∵ ,
, ,
,
∴ 平面
平面 ,
,
又∵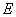 ,
,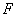 分别是
分别是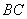 、
、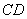 的中点,∴
的中点,∴
 ,
,
∴ 平面
平面 ,又
,又 平面
平面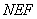 ,
,
∴平面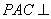 平面
平面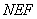 ; ---------------4分
; ---------------4分
(Ⅱ)连结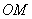 ,
,
∵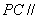 平面
平面 ,平面
,平面 平面
平面 ,
,
∴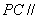
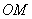 ,
,
∴ ,故
,故 -----------------8分
-----------------8分
(Ⅲ)∵ 平面
平面 ,
, 平面
平面 ,∴
,∴
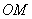 ,
,
在等腰三角形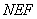 中,点
中,点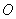 为
为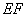 的中点,∴
的中点,∴ ,
,
∴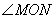 为所求二面角
为所求二面角 的平面角, ---------10分
的平面角, ---------10分
∵点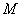 是
是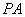 的中点,∴
的中点,∴ ,
,
所以在矩形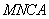 中,可求得
中,可求得 ,
,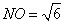 ,
, , --------12分
, --------12分
在 中,由余弦定理可求得
中,由余弦定理可求得 ,
,
∴二面角 的余弦值为
的余弦值为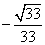 . --------------14分
. --------------14分
法2:(Ⅰ)同法1;
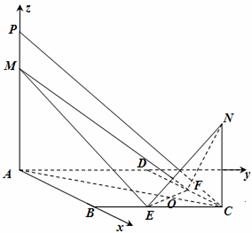
(Ⅱ)建立如图所示的直角坐标系,则 ,
,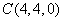 ,
, ,
, ,
,
∴ ,
, ,
,
设点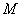 的坐标为
的坐标为 ,平面
,平面 的法向量为
的法向量为 ,则
,则 ,
,
所以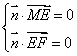 ,即
,即 ,令
,令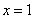 ,则
,则 ,
, ,
,
故 ,
,
∵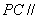 平面
平面 ,∴
,∴ ,即
,即 ,解得
,解得 ,
,
故 ,即点
,即点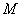 为线段
为线段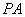 上靠近
上靠近 的四等分点;故
的四等分点;故 -------8分
-------8分
(Ⅲ) ,则
,则 ,设平面
,设平面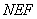 的法向量为
的法向量为 ,
,
 则
则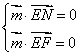 ,即
,即 ,令
,令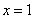 ,
,
则 ,
, ,即
,即 ,
,
当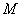 是
是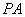 中点时,
中点时, ,则
,则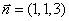 ,
,
∴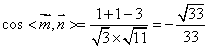 ,
,
∴二面角 的余弦值为
的余弦值为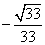 -----14分
-----14分


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为: ;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
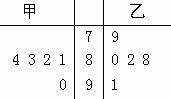
某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是 ;已知两位同学这5次成绩的平均数都是84,成绩比较稳定的是 (第二个空填“甲”或“ 乙”).
乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
A. (31,50) B. (32,47) C. (33,46) D. (34,42)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com