
分析:过B作圆C的切线BM交X轴于N,当D和M重合时,E和N重合,此时AE最大,因为△ABE的高OB一定时,此时△ABE的面积就最大,连接CF、CW,根据切线的性质证四边形CWOF是正方形,得到OW=CW=CF=OF=1,根据切线长定理推出BF=BM,NW=NM,设NW=NM=x,在Rt△BNO中由勾股定理得出BN
2=OB
2+ON
2,代入得到方程,求出x,即可求出AE的最大值,即可求出答案.
解答:过B作圆C的切线BM交X轴于N,当D和M重合时,E和N重合,此时AE最大,
因为△ABE的高OB一定时,此时△ABE的面积就最大,
连接CF、CW,
∵圆C且X轴于W,切Y轴于F,

∴CW⊥X轴,CF⊥Y轴,∵X轴⊥Y轴,
∵CF=CW,
∴四边形CWOF是正方形,
∴OW=CW=CF=OF=1,
∵BM切圆C于M,
∴BF=BM,NW=NM,
设NW=NM=x,则BN=

-1+1-x=

-x,
ON=1+x,
在Rt△BNO中由勾股定理得:BN
2=OB
2+ON
2,
∴

=
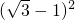
+(1+x)
2,
解得:x=2-

,
∴此时AE最大是

-1+1+2-

=2,
△ABE的最大面积是

×AE×OB=

×2×(

-1)=

-1,
故答案为:

-1.
点评:本题主要考查对切线的性质,切线长定理,勾股定理,三角形的面积,坐标与图形的性质,解一元一次方程,正方形的性质和判定等知识点的理解和掌握,熟练地运用性质进行计算是解此题的关键,题目比较典型,难度适中.

 如图,已知A,B两点的坐标分别为(
如图,已知A,B两点的坐标分别为( ,0),(0,
,0),(0, ),以点C(-1,-1)为圆心的⊙C分别与x轴,y轴都相切;若D是⊙C上的一个动点,线段DB与x轴交于点E.则△ABE的最大面积是________.
),以点C(-1,-1)为圆心的⊙C分别与x轴,y轴都相切;若D是⊙C上的一个动点,线段DB与x轴交于点E.则△ABE的最大面积是________.

 -1+1-x=
-1+1-x= -x,
-x, =
=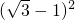 +(1+x)2,
+(1+x)2, ,
, -1+1+2-
-1+1+2- =2,
=2, ×AE×OB=
×AE×OB= ×2×(
×2×( -1)=
-1)= -1,
-1, -1.
-1.

 阅读快车系列答案
阅读快车系列答案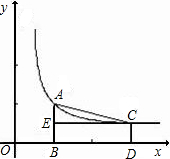 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(2
如图,已知A、B两点的坐标分别为(2 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.