
����Ŀ��������ȫ�ȵ����ǰ���ͼ1�ڷţ����С�A1CB1����ACB��90�㣬��A1����A��30�㣮
��1����ͼ1�С�A1B1C�Ƶ�C˳ʱ����ת45���ͼ2����P1��A1C��AB�Ľ��㣬��Q��A1B1��BC�Ľ��㣬��֤��CP1��CQ��
��2����ͼ2�У���AP1��a����CQ���ڶ��٣�
��3����ͼ2�С�A1B1C�Ƶ�C˳ʱ����ת����A2B2C����ͼ3������P2��A2C��AP1�Ľ��㣮����ת��Ϊ���ٶ�ʱ���С�AP1C�ס�CP1P2����ʱ�߶�CP1��P1P2֮�����һ��������������ϵ��
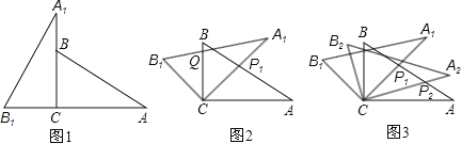
���𰸡���1��֤������������2��CQ��![]() a����3������P1CP2����P1AC��30��ʱ�� P1P2��
a����3������P1CP2����P1AC��30��ʱ�� P1P2��![]() CP1
CP1
�������������������1�����ݡ�A1B1C�͡�ABC��������ȫһ���������Σ�˳ʱ����ת45����������֤����B1CQ�ա�BCP1��Ȼ�����֤��CP1=CQ��
��2����P1D��AC��D�����ݡ�A=30����P1CD=45��ֱ����P1D=![]() AP1��CP1=
AP1��CP1=![]() P1D=
P1D=![]() AP1����AP1=a����CQ��
AP1����AP1=a����CQ��
��3������A P1C�ס�CP1P2ʱ����P1CP2=��P1AC=30�㣬�ٸ����������CP1��P1P2֮����ڵ�������ϵ��
���������
��1���ߡ�B1CB=45�㣬��B1CA1=90�㣬
���B1CQ=��BCP1=45�㣻
��B1C=BC����B1=��B��
���B1CQ�ա�BCP1��ASA��
��CQ=CP1��
��2����ͼ����P1D��AC��D��
�ߡ�A=30�㣬
��P1D=![]() AP1��
AP1��
�ߡ�P1CD=45�㣬
��![]() =sin45��=
=sin45��=![]() ��
��
��CP1=![]() P1D=
P1D=![]() AP1��
AP1��
��AP1=a��CQ=CP1��
��CQ=![]() a��
a��
��3������P1CP2=��P1AC=30��ʱ�����ڡ�CP1P2=��AP1C�����AP1C�ס�CP1P2��
���Խ�ͼ2�С�A1B1C�Ƶ�C˳ʱ����ת30�㵽��A2B2Cʱ���С�AP1C�ס�CP1P2��
��ʱ![]() =
=![]() =
=![]() ��
��
��P1P2=![]() CP1��
CP1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�Ƿ���x2+x-2020=0����������ʵ������a2+2a+b��ֵ��_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽����֪��
��֪ƽ������n��nΪ���ڻ����2��������������A1 �� A2 �� A3 �� ��An �� �ӵ�1����A1��ʼ��ֱ��������һ���㣬��ͬʱ��������������������ÿ�λ����ľ��붼���������n�λ�����ÿ����ȫ������һ�Σ��ۻ���n�κ����ص���1����A1 �� ���dzƴ˻���Ϊ�������˶������ҳ����е�Ϊ�������˶����Ļ����㣬�����n����ġ������˶�����·��֮��ΪSn ��
��1����ͼ1���������DZ߳�Ϊa�ĵȱ��������������㣬��ʱS3=��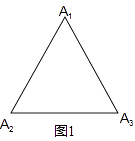
��2����ͼ2���������DZ߳�Ϊa���Խ��ߣ��߶�A1A2��A2A4����Ϊb���������ĸ����㣬��ʱS4= ��
���������
����n����ǡ����ͬһֱ���ϣ�����������붼Ϊ1��
��3����ͼ3����n=3ʱ��ֱ���ϵĵ�ֱ�ΪA1��A2��A3 ��
Ϊ����ɡ������˶����������IJ��������ͼ4��ʾ�����ַ�����
����1��A1��A3��A2��A1 �� ����2��A1��A2��A3��A1 ��
��������ȷ�ķ���Ϊ ��
A������1 B������2 C������1�ͷ���2
����ɴˡ������˶�����S3= �� 

��4����n�ֱ�ȡ4��5ʱ����Ӧ��S4= �� S5=
��5����ֱ������n���㣬���ú�n�Ĵ���ʽ��ʾSn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͩ���й���һ���Ľ�ħ�������������40%���ۣ�Ϊ�����������������������о�������۳��ۣ���ʱÿ��ħ�����ۼ�Ϊ28Ԫ��
��1����ħ���Ľ��ۣ�
��2����������һ������ø���˫ʮһ�������̵������ʣ�µ�ħ����ÿ3��80Ԫ�ļ۸���ۣ��ܿ�����һ�գ�����ħ�����й�����2800Ԫ����ó��й������Ľ�ħ�����ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��BD=2AD��E��F��G�ֱ���OC��OD��AB���е㣮���н��ۣ���EG=EF�� �ڡ�EFG�ա�GBE�� ��FBƽ�֡�EFG����EAƽ�֡�GEF�����ı���BEFG�����Σ�
������ȷ����.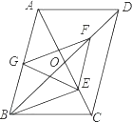
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽����һԪ���η���x2��4x=5ʱ���˷��̿ɱ���Ϊ�� ��
A.��x+2��2=1
B.��x��2��2=1
C.��x+2��2=9
D.��x��2��2=9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ԡ�ABC������Ϊ����BC��ͬ��ֱ��������ȱ������Σ�����ABD����BCE����ACF������ABC����ʲô����ʱ���ı���ADEF�����Σ��� �� 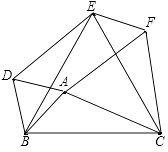
A.AB=AC
B.��BAC=90��
C.��BAC=120��
D.��BAC=150��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com