
分别以□ ABCD(![]() 90°) 的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
90°) 的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
 | |||
 | |||
解:(1)GF⊥EF,GF=EF.
(2)GF⊥![]() EF,GF=EF成立
EF,GF=EF成立
证明:∵四边形ABCD是平行四边形,
∴AB=DC,∠DAB+∠ADC=180°.
∵△ABE,△CDG,△ADF. 都是等腰直角三角形,
∴DG=AE,DF=AF,∠CDG=∠ADF=∠DAF=∠BAE=45°∴∠BAE+∠DAF+∠EAF+∠ADF+∠CDF =180°.
∴∠EAF+∠CDF =45°.
∵∠CDF+∠GDF =45°,
∴∠GDF=∠EAF.
∴△GDF≌△EAF.∴GF=EF,∠GFD=∠EFA.即∠GFD+∠GFA =∠EFA+∠GFA
∴∠GFE=∠DFA=90°.
∴GF⊥EF.


科目:初中数学 来源: 题型:
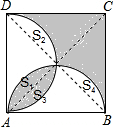 小华在某课外书上看到了这样一道题:“如图,分别以正方形ABCD的边AB、AD为直径画半圆.若正方形的边长为a,求阴影部分的面积.”从表面上看,图中的阴影部分是复杂且比较分散的图形,要直接计算它的面积还是有困难的,但小华仔细考虑过后,只是将正方形的对角线AC、BD连接起来,然后利用自己所学的“图形的旋转”知识很简便地就将本题解决了,你知道他是怎样做的吗?
小华在某课外书上看到了这样一道题:“如图,分别以正方形ABCD的边AB、AD为直径画半圆.若正方形的边长为a,求阴影部分的面积.”从表面上看,图中的阴影部分是复杂且比较分散的图形,要直接计算它的面积还是有困难的,但小华仔细考虑过后,只是将正方形的对角线AC、BD连接起来,然后利用自己所学的“图形的旋转”知识很简便地就将本题解决了,你知道他是怎样做的吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com