
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x-2}$ | B. | $\sqrt{2-x}$ | C. | -2$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| B. | 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% | |
| C. | 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| D. | 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
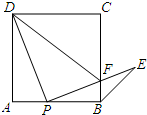 如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.
如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
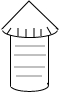 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com