
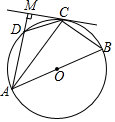
 如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )| A. | 20° | B. | 35° | C. | 40° | D. | 55° |
分析 由圆内接四边形的性质求出∠ADC=180°-∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠MCA=∠ABC=55°,由三角形的外角性质得出∠DCM=∠ADC-∠AMC=35°,即可求出∠ACD的度数.
解答 解:∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°-∠ABC=125°,∠BAC=90°-∠ABC=35°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=55°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC-∠AMC=35°,
∴∠ACD=∠MCA-∠DCM=55°-35°=20°;
故选:A.
点评 本题考查了圆内接四边形的性质、圆周角定理、三角形的外角性质、弦切角定理等知识;熟练掌握圆内接四边形的性质和圆周角定理是解决问题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
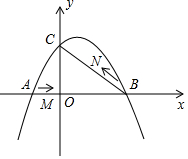 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k<1 | C. | k≥1 | D. | k≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.
如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.
如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com