
【题目】为了庆祝祖国70岁生日,阳光中学举行“向祖国70岁生日献礼”系列活动。学校团委为了组织好大型团体操表演,随机抽查部分七年级学生的身高,将学生身高分成四个组,并绘制成如下不完整的统计图表。
组别 | 身高 | 人数 |
1组 |
| 15 |
2组 |
|
|
3组 |
|
|
4组 |
| 10 |
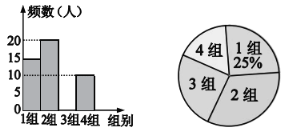
根据以上信息,解答下列问题:
(1)在统计表中,![]() 的值是________;本次调查的学生人数是________人.
的值是________;本次调查的学生人数是________人.
(2)补全频数分布直方图.
(3)在“祖国万岁”方队中,列队形成“祖国”二字学生的身高应该在![]() 的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人?
的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人?
【答案】(1)20,60;(2)详见解析;(3)身高符合该条件的学生约有200人.
【解析】
(1)由条形统计图可知第二组的人数即![]() 的值,用第一组的人数除以其所占的百分比即为本次调查的学生人数;(2)本次调查的学生人数减去第一、二、四组的人数即为第三组人数;(3)先求出身高在
的值,用第一组的人数除以其所占的百分比即为本次调查的学生人数;(2)本次调查的学生人数减去第一、二、四组的人数即为第三组人数;(3)先求出身高在![]() 的范围内的人数所占样本的百分比,再由样本估计总体即可.
的范围内的人数所占样本的百分比,再由样本估计总体即可.
解:(1)由条形统计图可知第二组的人数为20,所以![]() 的值为20;
的值为20;
本次调查的学生人数![]() (人);
(人);
(2)第三组的人数![]() (人),频数分布直方图补充如下:
(人),频数分布直方图补充如下:
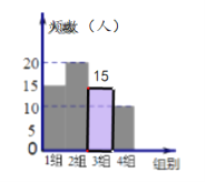
(3)由(1)、(2)知,在被调查的学生中,
身高在![]() 的人数是
的人数是![]() (人)
(人)
估计该校七年级480名学生中,身高符合该条件的学生约有![]() (人)
(人)
答:身高符合该条件的学生约有200人.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() .点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )
.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )

A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.动点E、F同时从点B出发,点E沿折线 BA–AD–DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.
请根据图中的信息,解答下列问题:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字说明点N所表示的实际意义;
(3)直接写出当自变量t为何值时,函数y的值等于5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清朝数学家梅文鼎的著作《方程论》中有这样一道题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,
每亩场地折实田多少?
译文为:假如有山田3亩,场地6亩,其产粮相当于实田4.7亩;又山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?请你解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市文化底蕴深厚,旅游资源丰富,天心阁、岳麓山、橘子洲三个景区是人们节假日游玩的热点景区,李老师对九年级1班学生五一长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B、游两个景区;C、游一个景区;D、不到这三个景区游玩.现根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题:
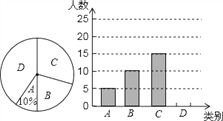
(1)九(1)班共有学生 人,请将条形统计图补充完整;
(2)在扇形统计图中,表示“B类别”的扇形的圆心角的度数为 ;
(3)若小明、小华两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,请用列表或者画树状图的形式求出他们同时选中岳麓山的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三位数,十位数字是![]() ,百位数字是十位数字的2倍,个位数字比十位数字小2.
,百位数字是十位数字的2倍,个位数字比十位数字小2.
(1)试用代数式表示出这个三位数.
(2)试写出所有符合条件的三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则
(x2﹣1)=y2,原方程化为y2﹣5y+4=0.①
解得y1=1,y2=4
当y=1时,x2﹣1=1.∴x2=2.∴x=±![]() ;
;
当y=4时,x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]()
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想.
(2)解方程:x4﹣x2﹣6=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com