
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
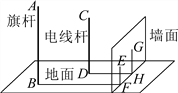
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
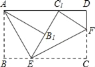
A. ![]() B. 2 C. 3 D. 2
B. 2 C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校奖励学生,初一获奖学生中,有一人获奖品3件,其余每人获奖品7件;初二获奖学生中,有一人获奖品4件,其余每人获奖品9件.如果两个年级获奖人数不等,但奖品数目相等,且每个年级奖品数大于50而不超过100,那么两个年级获奖学生共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
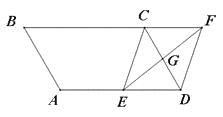
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
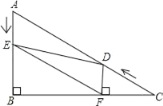
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( )
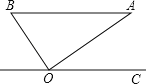
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54°
查看答案和解析>>
科目:初中数学 来源: 题型:
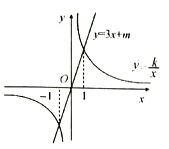
【题目】将直线y=3x+1向下平移1个单位长度,得到直线y=3x +m,若反比例函数![]() 的图象与直线y=3x+m相交于点A,且点A 的纵坐标是3.
的图象与直线y=3x+m相交于点A,且点A 的纵坐标是3.
(1)求m和k的值;
(2) 直接写出方程![]() 的解:
的解:
(3) 结合图象求不等式![]() 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com