
【题目】如图1,两块直角三角纸板(Rt△ABC和Rt△BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB=90°,∠ABC=30°,BD=DE=AC=2.将△BDE绕着点B顺时针旋转.
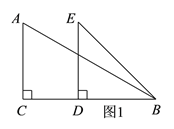
(1)当点D在BC上时,求CD的长;
(2)当△BDE旋转到A,D,E三点共线时,求△CDE的面积;
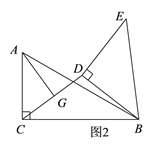
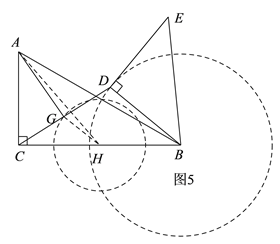
(3)如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.
【答案】(1)![]() ;(2)△CDE的面积为1或2;(3)
;(2)△CDE的面积为1或2;(3)![]() ,
,![]() .
.
【解析】分析:
(1)由已知条件易得AB=2AC=4结合AC=2及∠ACB=90°可得BC=![]() ,由此可得CD=BC-BD=
,由此可得CD=BC-BD=![]() ;
;
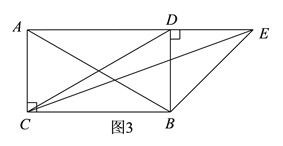
(2)根据题意分以下两种情况,画出图形,结合已知条件分析计算即可:①点D在BC上方,如图3;②点D在BC下方,如图4;
(3)如图5,取BC的中点H,连接GH、AH,由已知条件易得AH=![]() ,GH=
,GH=![]() BD=1,由题意和图可知:点G在以点H为圆心,GH为半径的⊙H上运动,点D在以B为圆心,BD为半径的⊙B上运动,由此即可得到AG的最大值和最小值.
BD=1,由题意和图可知:点G在以点H为圆心,GH为半径的⊙H上运动,点D在以B为圆心,BD为半径的⊙B上运动,由此即可得到AG的最大值和最小值.
详解:
(1)∵在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,
∴AB=2AC=4,
∴BC=![]() ;
;
∵BD=2,点D在BC上,
∴CD=BC-BD=![]() ;
;
(2)①如图3,当点D在BC上方,A、D、E三点共线时,
∵A、D、E三点共线,∠BDE=90°,
∴∠ADE=90°=∠ACB,
又∵AB=BA,AC=BD,
∴△ABC≌△BAD,
∴AD=BC,
∴四边形ACBD是平行四边形,
又∵∠ACB=90°,
∴四边形ACBD是矩形,
∴![]() ;
;
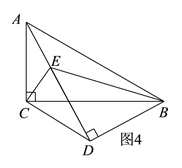
②如图4,当点D在BC下方,A、D、E三点共线时,
∵BD=DE=AC,
∴∠BAD=∠ABC=30°,所以∠CAD=∠CBD=30°,
∵△ABC和△ABD中,∠ACB=∠ADB=90°,
∴A、C、D、B四点共圆,
∴∠BCD=∠ADC=30°,
∴∠BCD=∠CBD,
∴CD=DE=BD=2,
∴![]() ,
,
综上所述△CDE的面积为1或2;
(3)如图5,由题意可知,随着△BDE绕着点B进行顺时针旋转,点D的运动路线是以点B为圆心,BD为半径的圆,取BC的中点H,连接GH,AH,
∴CH=![]() BC=
BC=![]() ,
,
∴AH=![]() ,
,
∴GH是△BCD的中位线,
∴GH=![]() BD=1,
BD=1,
∴点G的运动路线是以H为圆心,1为半径的圆,
∴AG的最大值=AH+1=![]() +1,AG的最小值=AH-1=
+1,AG的最小值=AH-1=![]() -1.
-1.


科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
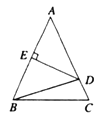
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于点D、E,若△ABC和△BDC 的周长分别为40cm和25cm ,则BC=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜梁永辉商场今年二月份以每桶40元的单价购进1000桶甲、乙两种食用油,然后以甲种食用油每桶75元、乙桶食用油每桶60元的价格售完,共获利29000元.
(1)求该商场分别购进甲、乙两种食用油多少桶?
(2)为了增加销售量,获得最大利润,根据销售情况和市场分析,在进价不变的情况下该经销商决定调整价格,将甲种食用油的价格在二月份的基础上下调20%,乙种食用油的价格上涨![]() a%,但甲的销售量还是较二月下降了
a%,但甲的销售量还是较二月下降了![]() a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在用黑色围棋进行摆放图案的游戏中,一同学摆放了如下图案,请根据图中信息完成下列的问题:
 ...
...
(1)填写下表:
图形编号 | ① | ② | ③ | … | … |
图中棋子的总数 | ________ | ________ | ________ | … | … |
(2)第10个图形中棋子为________颗围棋;
(3)该同学如果继续摆放下去,那么第![]() 个图案要用________颗围棋;
个图案要用________颗围棋;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com