
【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=![]() ∠COF.
∠COF.

(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
信息读取
(1)梯形上底的长AB=;
(2)直角梯形ABCD的面积=;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
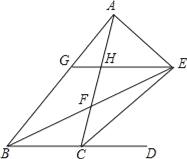
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
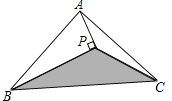
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
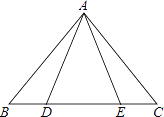
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com