
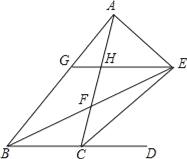
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
【答案】①③④.
【解析】
①根据角平分线的定义得到∠EBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACD,根据外角的性质即可得到结论;
∠ACD,根据外角的性质即可得到结论;
②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;
③由BG=GE,CH=EH,于是得到BG-CH=GE-EH=GH.即可得到结论;
④由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.
①BE平分∠ABC,
∴∠EBC=![]() ∠ABC,
∠ABC,
∵CE平分∠ACD,
∴∠DCE=![]() ∠ACD,
∠ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=![]() (∠BAC+∠ABC)=∠EBC+
(∠BAC+∠ABC)=∠EBC+![]() ∠BAC,
∠BAC,
∴∠BEC=![]() ∠BAC,故①正确;
∠BAC,故①正确;
∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所以不能得出全等的结论,故②错误;
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BGCH=GEEH=GH,
∴BG=CH+GH,
故③正确;
④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
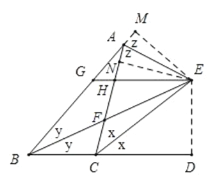
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180![]() 2z,∠ACB=180
2z,∠ACB=180![]() 2x,
2x,
∵∠ABC+∠ACB+∠BAC=180![]() ,
,
∴2y+180![]() 2z+180
2z+180![]() 2x=180
2x=180![]() ,
,
∴x+z=y+90![]() ,
,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90![]() ,
,
∴x+∠AEB=90![]() ,
,
即∠ACE+∠AEB=90![]() ,
,
故④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成![]() 已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
![]() 求甲、乙两工程队每天能完成道路的长度分别是多少m?
求甲、乙两工程队每天能完成道路的长度分别是多少m?
![]() 若村委每天需付给甲队的道路改造费用为
若村委每天需付给甲队的道路改造费用为![]() 万元,乙队为
万元,乙队为![]() 万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC 
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:![]() =
=![]() (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例:![]() =
=![]()
(1)计算:![]() =__;
=__;![]() =__;
=__;
(2)如果![]() =
=![]() ,那么p=__;如果
,那么p=__;如果![]() =
=![]() ,那么a=__;
,那么a=__;
(3)如果![]() =
=![]() ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )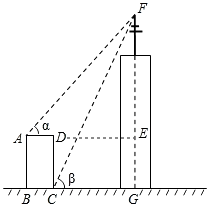
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com