
【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在D′处.若AB=3,BC=9,则折痕EF的长为( ) 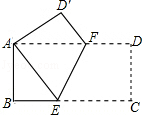
A.![]()
B.4
C.5
D.2 ![]()
【答案】A
【解析】解:∵矩形ABCD沿EF折叠,点C落在A处, ∴AE=EC,∠AEF=∠CEF,
设AE=x,则BE=BC﹣EC=9﹣x,
在Rt△ABE中,根据勾股定理得,AB2+BE2=AE2 ,
即32+(9﹣x)2=x2 ,
解得x=5,
所以,AE=5,BE=9﹣5=4,
∵矩形对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=5,
过点E作EG⊥AD于G,则四边形ABEG是矩形,
∴AG=BE=4,
GF=AF﹣AG=5﹣4=1,
在Rt△EFG中,根据勾股定理得,EF= ![]() =
= ![]() =
= ![]() .
.
故选A.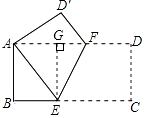
根据翻折的性质可得AE=EC,∠AEF=∠CEF,设AE=x,表示出BE,在Rt△ABE中,利用勾股定理列方程求出x,根据两直线平行,内错角相等可得∠AFE=∠CEF,从而得到∠AEF=∠AFE,根据等角对等边可得AF=AE,过点E作EG⊥AD于G,求出AG、GF,再利用勾股定理列式计算即可得解.


科目:初中数学 来源: 题型:
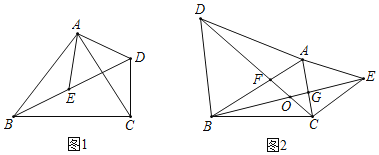
【题目】(1)问题发现:如图1,如果△ABC和△ADE均为等边三角形(等边三角形的三条边都相等,三个角都是60°),点B、E、D三点在同一直线上,连接CD.则CD与BE的数量关系为______;∠BDC的度数为______度.
(2)探究:如图2,若△ABC为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出∠BOD的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
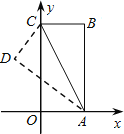
【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置.若点B的坐标为(2,4),则点D的横坐标是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两个全等直角三角形的直角顶点及一条直角边重合,将△ABC绕点C按顺时针方向旋转到△A′CB′的位置,其中A′C交直线AD于点E,A′B′分别交直线AD,AC于点F,G.则旋转后的图中,全等三角形共有( )
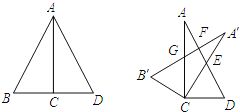
A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
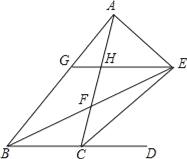
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
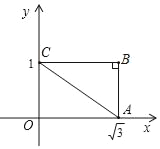
【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(![]() ,0),C(0,1).
,0),C(0,1).
(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com