
【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
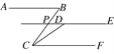
【题目】如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°.
(1)试判断∠ABP与∠BPD之间的数量关系,并说明理由;
(2)求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴的正半轴上,且三角形OAB的面积为2,求点A的坐标;
(2)若点A(3,0),BC∥OA,BC=OA,求点C的坐标;
(3)若点A(3,0),点D(3,-4),求四边形ODAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com