
����Ŀ��ij��ѧΪ�ﱸУ������ӡ��һ��У�����ᣬ�ü����ÿ����Ҫ10��8K��С��ֽ������4��Ϊ��ɫҳ��6��Ϊ�ڰ�ҳ��ӡ�Ƹü������ܷ������ư�Ѻ�ӡˢ����������ɣ��ư����ӡ���أ��۸�Ϊ����ɫҳ300Ԫ/�ţ��ڰ�ҳ50Ԫ/�ţ�ӡˢ����ӡ���Ĺ�ϵ������
ӡ��a������λ��ǧ�ᣩ | 1��a��5 | 5��a��10 |
��ɫ������λ��Ԫ/�ţ� | 2.2 | 2.0 |
�ڰף���λ��Ԫ/�ţ� | 0.7 | 0.6 |
(1)ֱ��д��ӡ�������������ư��Ϊ����Ԫ��
(2)��ӡ��6ǧ�ᣬ��ô������ٷ��ã�
(3)��ӡ��x��1��x��10��ǧ�ᣬ�������ΪyԪ����д��y��x֮��Ĺ�ϵʽ��
���𰸡���1��1500Ԫ����2������71100Ԫ�ķ�������3��y=![]() ��
��
��������
��1�������ư��=��ɫҳ�ư��+�ڰ�ҳ�ư�ѣ��������ݼ��������
��2�������ܷ���=�ư��+ӡˢ�ѣ��������ݼ��������
��3����![]() ��
��![]() ��������ҳ�y����x�ĺ�����ϵʽ���ϲ���һ�ɵó�����.
��������ҳ�y����x�ĺ�����ϵʽ���ϲ���һ�ɵó�����.
�⣺��1��ӡ�������������ư��Ϊ��300��4+50��6=1500��Ԫ����
��ӡ�������������ư��Ϊ1500Ԫ��
��2��ӡ��6ǧ��ʱ����Ҫ�ķ���Ϊ��1500+��2��4+0.6��6����6000=71100��Ԫ����
����ӡ��6ǧ�ᣬ��ô����71100Ԫ�ķ��ã�
��3������֪�ã�
��1��x��5ʱ��y=1500+��2.2��4+0.7��6����1000x=13000x+1500��
��5��x��10ʱ��y=1500+��2��4+0.6��6����1000x=11600x+1500��
���Ͽ�֪��y��x֮��Ĺ�ϵʽΪy=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ�����֪������C1��y1=��x2+ax+b��������C2��y2=2x2+4x+6Ϊ���Ѻ������ߡ���������C1��x�ύ�ڵ�A��C����y�ύ�ڵ�B��
��1����������C1�ı���ʽ��
��2����F��t��0������3��t��0����x���ϵ�һ�㣬����F��x��Ĵ��߽����������P����ֱ��AB�ڵ�E������P��PD��AB�ڵ�D��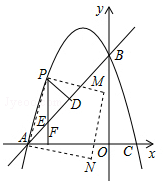
���Ƿ���ڵ�F��ʹPE+PD��ֵ��������ڣ������t��ֵ���������ڣ���˵�����ɣ�
������PA����APΪ����ͼʾһ���������APMN�����ŵ�F���˶��������εĴ�С��λ��Ҳ��֮�ı䣮��������APMN�еı�MN��y�����ҽ���һ������ʱ����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
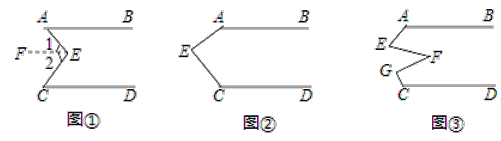
����Ŀ������֪����ͼ����AB��CD����E��ֱ��AB��CD֮�䣬����AE��BE����˵����BEE+��DCE����AEC����������������Ľ�����̣����������Ľ�����̣�����գ����ɻ���ѧʽ����
�⣺��ͼ�٣�����E��EF��AB
���BAE����1���� ����
��AB��CD���� ����
��CD��EF���� ����
���2����DCE
���BAE+��DCE����1+��2���� ����
���BAE+��DCE����AEC
��̽��������E����ͼ�ڵ�λ��ʱ�������������䣬��˵����AEC+��FGC+��DCE��360�㣻
��Ӧ�ã���E��F��G��ֱ��AB��CD֮�䣬����AE��EF��FG��CG�������������䣬��ͼ�ۣ�����EFG��36�������BAE+��AEF+��FGC+��DCG���� ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
ij�̳���8��Ԫ����һ���¿�������ϼܺ�ܿ�����һ�գ��̳��ֽ��������ڶ������ֳ����������ǵ�һ�ε�2��������������4Ԫ/�����������ȥ17.6��Ԫ��
��1�����̳���һ�������������ټ���
��2���̳��������ֳ���ʱ��ÿ�����۶���58Ԫ��ʣ��150��ʱ�����۳��ۣ�ȫ�����꣮�����������������̳���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС����ѧϰ�ˡ�������Ǻ������Ժ�չ��������߶ȵ�ʵ���������һ������CD�ĸ߶ȣ�����վ��B������¥��C���������Ϊ30�㣬���������﷽����20m�������F�����¥��C������Ϊ45�㣨BFD��ͬһֱ���ϣ�����֪�۲�Ա���۾���������Ϊ1.5m����AB=1.5m�������ⶰ������CD�ĸ߶ȣ����ο����ݣ� ![]() ��1.732��
��1.732�� ![]() ��1.414���������������
��1.414���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�̽��
֪ʶ�ۼ�
�ⷽ����![]()
�⣺��a��1=x��b+2=y��ԭ������ɱ�Ϊ![]()
�ⷽ����ã�![]() ��
��![]() ����
����![]() ���ֽⷽ����ķ����л�Ԫ����
���ֽⷽ����ķ����л�Ԫ����
��1����չ���
�����������������з����飺
��2����������
��֪����x��y�ķ�����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��ֱ��д������m��n�ķ�����
��ֱ��д������m��n�ķ�����![]() �Ľ�Ϊ_____________��
�Ľ�Ϊ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������D������Ϊ����3��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��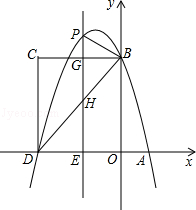
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�Ϸ�ʱ�����ú�m�Ĵ���ʽ��ʾPG�ij��ȣ�
��3���ڣ�2���������£��Ƿ���������ĵ�P��ʹ����P��B��GΪ��������������DEH���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
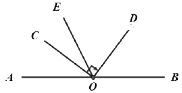
����Ŀ����֪��A��O��B��һ��ֱ����,������OC��O��˳ʱ�뷽����ת90���,�õ�����OD,����ת������,����OCʼ����ֱ��AB�Ϸ�,��OEƽ�֡�AOD.Լ��,���ۡ�AOD��С���,OE����������OA��OD�����γɵ���С�ǵ�ƽ����.
(1)��ͼ,����AOC=30��ʱ,��BOD=_________�㣻
(2)������OFƽ�֡�BOC,���EOF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=30�㣬OPƽ����AOB��PD��OB��D��PC��OB��OA��C����PC=10����PD=________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com