
【题目】如图,矩形ABCD中,AB= ![]() ,BC=
,BC= ![]() ,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则
,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则 ![]() 等于( )
等于( ) 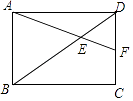
A.![]()
B.![]()
C.![]()
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
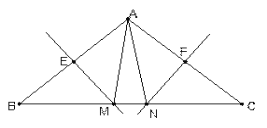
【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
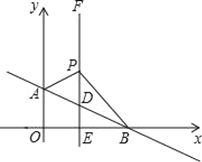
【题目】如图,平面直角坐标系中,直线AB:y=﹣![]() x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
(1)直线AB的表达式为__________________;
(2)①求△ABP的面积(用含n的代数式表示);
②当S△ABP=2时,求点P的坐标;
③在②的条件下,以PB为边在第一象限作等腰直角三角形BPC,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴的正半轴上,且三角形OAB的面积为2,求点A的坐标;
(2)若点A(3,0),BC∥OA,BC=OA,求点C的坐标;
(3)若点A(3,0),点D(3,-4),求四边形ODAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
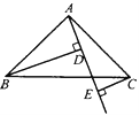
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
(1)AD与CE的大小关系如何?请说明理由;
(2)若BD=5,CE=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com