
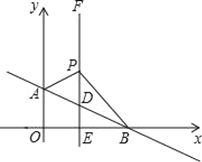
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌжБЯпABЃКy=Љ![]() x+bНЛyжсгкAЃЈ0ЃЌ1ЃЉЃЌНЛxжсгкЕуBЃЎЙ§ЕуEЃЈ1ЃЌ0ЃЉзїxжсЕФДЙЯпEFНЛABгкЕуDЃЌPЪЧжБЯпEFЩЯвЛЖЏЕуЃЌЧвдкЕуDЕФЩЯЗНЃЌЩшPЃЈ1ЃЌnЃЉЃЎ
x+bНЛyжсгкAЃЈ0ЃЌ1ЃЉЃЌНЛxжсгкЕуBЃЎЙ§ЕуEЃЈ1ЃЌ0ЃЉзїxжсЕФДЙЯпEFНЛABгкЕуDЃЌPЪЧжБЯпEFЩЯвЛЖЏЕуЃЌЧвдкЕуDЕФЩЯЗНЃЌЩшPЃЈ1ЃЌnЃЉЃЎ
ЃЈ1ЃЉжБЯпABЕФБэДяЪНЮЊ__________________ЃЛ
ЃЈ2ЃЉЂйЧѓЁїABPЕФУцЛ§ЃЈгУКЌnЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЂкЕБSЁїABP=2ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂлдкЂкЕФЬѕМўЯТЃЌвдPBЮЊБпдкЕквЛЯѓЯозїЕШбќжБНЧШ§НЧаЮBPCЃЌЧыжБНгаДГіЕуCЕФзјБъЃЎ
ЁОД№АИЁП(1)y=Љ![]() x+1ЃЛ(2)ЂйSЁїABP=
x+1ЃЛ(2)ЂйSЁїABP=![]() ЃЛЂкPЃЈ1ЃЌ2ЃЉЃЛЂлЃЈ3ЃЌ4ЃЉЛђЃЈ5ЃЌ2ЃЉЛђЃЈ3ЃЌ2ЃЉЃЎ
ЃЛЂкPЃЈ1ЃЌ2ЃЉЃЛЂлЃЈ3ЃЌ4ЃЉЛђЃЈ5ЃЌ2ЃЉЛђЃЈ3ЃЌ2ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉАбAЕФзјБъДњШыжБЯпABЕФНтЮіЪНМДПЩЧѓЕУbЕФжЕЃЌгЩДЫМДПЩЧѓЕУжБЯпABЕФНтЮіЪНЃЛЃЈ2ЃЉЂйЙ§ЕуAзїAMЁЭPDЃЌДЙзуЮЊMЃЌЧѓЕУAMЕФГЄЃЌдйЧѓЕУЁїBPDКЭЁїPABЕФУцЛ§ЃЌЖўепЕФКЭМДЮЊЁїABPЕФУцЛ§ЃЛЂкЕБSЁїABP=2ЪБЃЌДњШыЂйжаЫљЕУЕФДњЪ§ЪНЃЌЧѓЕУnжЕЃЌМДПЩЧѓЕУЕуPЕФзјБъЃЛЂлЗжPЪЧжБНЧЖЅЕуЧвBP=PCЁЂBЪЧжБНЧЖЅЕуЧвBP=BC ЁЂCЪЧжБНЧЖЅЕуЧвCP=CBШ§жжЧщПіЧѓЕуCЕФзјБъМДПЩЃЎ
ЃЈ1ЃЉЁпy=-![]() x+bОЙ§AЃЈ0ЃЌ1ЃЉЃЌ
x+bОЙ§AЃЈ0ЃЌ1ЃЉЃЌ
Ёрb=1ЃЌ
ЁржБЯпABЕФНтЮіЪНЪЧy=-![]() x+1ЃЛ
x+1ЃЛ
ЙЪД№АИЮЊЃКy=-![]() x+1ЃЛ
x+1ЃЛ
ЃЈ2ЃЉЂйЙ§ЕуAзїAMЁЭPDЃЌДЙзуЮЊMЃЌдђгаAM=1ЃЌ
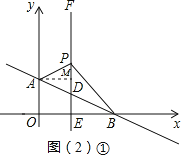
Ёпx=1ЪБЃЌy=-![]() x+1=
x+1=![]() ЃЌPдкЕуDЕФЩЯЗНЃЌ
ЃЌPдкЕуDЕФЩЯЗНЃЌ
ЁрPD=n-![]() ЃЌSЁїAPD=
ЃЌSЁїAPD=![]() PDAM=
PDAM=![]() ЁС1ЁСЃЈn
ЁС1ЁСЃЈn![]() ЃЉ=
ЃЉ=![]() n
n![]() ЃЌ
ЃЌ
гЩЕуBЃЈ3ЃЌ0ЃЉЃЌПЩжЊЕуBЕНжБЯпx=1ЕФОрРыЮЊ2ЃЌМДЁїBDPЕФБпPDЩЯЕФИпГЄЮЊ2ЃЌ
ЁрSЁїBPD=![]() PDЁС2=n-
PDЁС2=n-![]() ЃЌ
ЃЌ
ЁрSЁїPAB=SЁїAPD+SЁїBPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1ЃЛ
n-1ЃЛ
ЂкЕБSЁїABP=2ЪБЃЌ![]() n-1=2ЃЌ
n-1=2ЃЌ
НтЕУn=2ЃЌ
ЁрЕуPЃЈ1ЃЌ2ЃЉЃЎ
ЂлЁпEЃЈ1ЃЌ0ЃЉЃЌ
ЁрPE=BE=2ЃЌ
ЁрЁЯEPB=ЁЯEBP=45ЁуЃЎ
Ек1жжЧщПіЃЌШчЭМ1ЃЌЁЯCPB=90ЁуЃЌBP=PCЃЌ
Й§ЕуCзїCNЁЭжБЯпx=1гкЕуNЃЎ
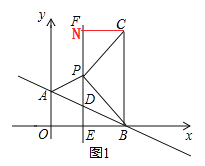
ЁпЁЯCPB=90ЁуЃЌЁЯEPB=45ЁуЃЌ
ЁрЁЯNPC=ЁЯEPB=45ЁуЃЌ
дкЁїCNPгыЁїBEPжаЃЌ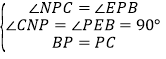 ЃЌ
ЃЌ
ЁрЁїCNPЁеЁїBEPЃЌ
ЁрPN=NC=EB=PE=2ЃЌ
ЁрNE=NP+PE=2+2=4ЃЌ
ЁрCЃЈ3ЃЌ4ЃЉЃЎ
Ек2жжЧщПіЃЌШчЭМ2ЃЌЁЯPBC=90ЁуЃЌBP=BCЃЌ
Й§ЕуCзїCFЁЭxжсгкЕуFЃЎ
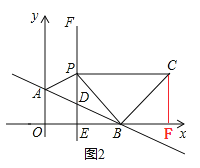
ЁпЁЯPBC=90ЁуЃЌЁЯEBP=45ЁуЃЌ
ЁрЁЯCBF=ЁЯPBE=45ЁуЃЌ
дкЁїCBPгыЁїPBEжаЃЌ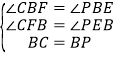 ЃЌ
ЃЌ
ЁрЁїCBFЁеЁїPBEЃЎ
ЁрBF=CF=PE=EB=2ЃЌ
ЁрOF=OB+BF=3+2=5ЃЌ
ЁрCЃЈ5ЃЌ2ЃЉЃЎ
Ек3жжЧщПіЃЌШчЭМ3ЃЌЁЯPCB=90ЁуЃЌCP=CBЃЌ
ЁрЁЯCPB=ЁЯCBP=45ЁуЃЌ
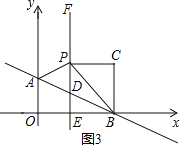
ЁпЁЯEPB=ЁЯEBP=45ЁуЃЌ
ЁрЁЯPCB=ЁЯCBE=ЁЯEPC=90ЁуЃЌ
ЁрЫФБпаЮEBCPЮЊОиаЮЃЌ
ЁпCP=CBЃЌ
ЁрЫФБпаЮEBCPЮЊе§ЗНаЮЃЌ
ЁрPC=CB=PE=EB=2ЃЌ
ЁрCЃЈ3ЃЌ2ЃЉЃЎ
ЁрвдPBЮЊБпдкЕквЛЯѓЯозїЕШбќжБНЧШ§НЧаЮBPCЃЌЕуCЕФзјБъЪЧЃЈ3ЃЌ4ЃЉЛђЃЈ5ЃЌ2ЃЉЛђЃЈ3ЃЌ2ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊСНИіШЋЕШжБНЧШ§НЧаЮЕФжБНЧЖЅЕуМАвЛЬѕжБНЧБпжиКЯЃЌНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊЕНЁїAЁфCBЁфЕФЮЛжУЃЌЦфжаAЁфCНЛжБЯпADгкЕуEЃЌAЁфBЁфЗжБ№НЛжБЯпADЃЌACгкЕуFЃЌGЃЎдђа§зЊКѓЕФЭМжаЃЌШЋЕШШ§НЧаЮЙВгаЃЈЁЁЁЁЃЉ
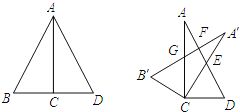
A. 2Жд B. 3Жд C. 4Жд D. 5Жд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
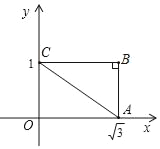
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌЁЯACBЃН30ЁуЃЌЦфжБНЧБпЗжБ№гызјБъжсДЙжБЃЌвбжЊЖЅЕуЕФзјБъЮЊAЃЈ![]() ЃЌ0ЃЉЃЌCЃЈ0ЃЌ1ЃЉЃЎ
ЃЌ0ЃЉЃЌCЃЈ0ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉШчЙћAЙигкBCЖдГЦЕФЕуЪЧDЃЌдђЕуDЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЙ§ЕуBзїжБЯпmЁЮACЃЌНЛCDСЌЯпгкEЃЌЧѓЁїBCEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮAB=![]() (
(![]() ЮЊГЃЪ§)ЃЌЕуCЮЊжБЯпABЩЯвЛЕуЃЌЕуPЁЂQЗжБ№дкЯпЖЮBCЁЂACЩЯЃЌЧвТњзуCQ=2AQЃЌCP=2BP.
ЮЊГЃЪ§)ЃЌЕуCЮЊжБЯпABЩЯвЛЕуЃЌЕуPЁЂQЗжБ№дкЯпЖЮBCЁЂACЩЯЃЌЧвТњзуCQ=2AQЃЌCP=2BP.
(1)ШчЭМЃЌЕБЕуCЧЁКУдкЯпЖЮABжаЕуЪБЃЌдђPQ=_______(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
(2)ШєЕуCЮЊжБЯпABЩЯШЮвЛЕуЃЌдђPQГЄЖШЪЧЗёЮЊГЃЪ§?ШєЪЧЃЌЧыЧѓГіетИіГЃЪ§ЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
(3)ШєЕуCдкЕуAзѓВрЃЌЭЌЪБЕуPдкЯпЖЮABЩЯ(ВЛгыЖЫЕужиКЯ)ЃЌЧыХаЖЯ2AP+CQ-2PQгы1ЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЁЃ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌЖЅЕуAЕФзјБъЮЊЃЈ4ЃЌ3ЃЉ 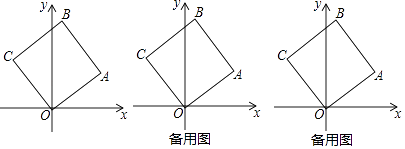
ЃЈ1ЃЉЖЅЕуCЕФзјБъЮЊЃЈ ЃЌ ЃЉЃЌЖЅЕуBЕФзјБъЮЊЃЈ ЃЌ ЃЉЃЛ
ЃЈ2ЃЉЯжгаЖЏЕуPЁЂQЗжБ№ДгCЁЂAЭЌЪБГіЗЂЃЌЕуPбиЯпЖЮCBЯђжеЕуBдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛЃЌЕуQбиелЯпAЁњOЁњCЯђжеЕуCдЫЖЏЃЌЫйЖШЮЊУПУыkИіЕЅЮЛЃЌЕБдЫЖЏЪБМфЮЊ2УыЪБЃЌвдPЁЂQЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓДЫЪБkЕФжЕЃЎ
ЃЈ3ЃЉШєе§ЗНаЮOABCвдУПУы ![]() ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕНxжсЩЯЪБЭЃжЙЯТЛЌЃЎЩше§ЗНаЮOABCдкxжсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕНxжсЩЯЪБЭЃжЙЯТЛЌЃЎЩше§ЗНаЮOABCдкxжсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧЁїABCжаЃЌAB=AC=8ЃЌвдABЮЊжБОЖЕФАыдВOНЛаББпBCгкDЃЌдђвѕгАВПЗжУцЛ§ЮЊЃЈНсЙћБЃСєІаЃЉЃЈ ЃЉ 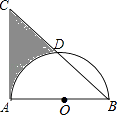
A.16
B.24Љ4Іа
C.32Љ4Іа
D.32Љ8Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB= ![]() ЃЌBC=
ЃЌBC= ![]() ЃЌЕуEдкЖдНЧЯпBDЩЯЃЌЧвBE=1.8ЃЌСЌНгAEВЂбгГЄНЛDCгкFЃЌдђ
ЃЌЕуEдкЖдНЧЯпBDЩЯЃЌЧвBE=1.8ЃЌСЌНгAEВЂбгГЄНЛDCгкFЃЌдђ ![]() ЕШгкЃЈ ЃЉ
ЕШгкЃЈ ЃЉ 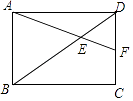
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
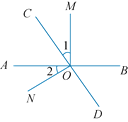
ЁОЬтФПЁПШчЭМЃЌжБЯпABЃЌCDЯрНЛгкЕуOЃЌЙ§ЕуOзїСНЬѕЩфЯпOMЃЌONЃЌЧвЁЯAOMЃНЁЯCONЃН90Ёу.
(1)ШєOCЦНЗжЁЯAOMЃЌЧѓЁЯAODЕФЖШЪ§ЃЛ
(2)ШєЁЯ1ЃНЁЯBOCЃЌЧѓЁЯAOCКЭЁЯMOD.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁбOЕФФкНгЫФБпаЮACDBжаЃЌABЮЊжБОЖЃЌACЃКBC=1ЃК2ЃЌЕуDЮЊЛЁABЕФжаЕуЃЌBEЁЭCDДЙзуЮЊEЃЎ 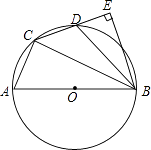
ЃЈ1ЃЉЧѓЁЯBCEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃКDЮЊCEЕФжаЕуЃЛ
ЃЈ3ЃЉСЌНгOEНЛBCгкЕуFЃЌШєAB= ![]() ЃЌЧѓOEЕФГЄЖШЃЎ
ЃЌЧѓOEЕФГЄЖШЃЎ 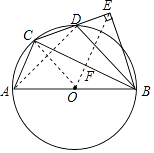
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com