
 的图象与反比例函数
的图象与反比例函数 的图象交于点A(1,m),与x轴交于点
的图象交于点A(1,m),与x轴交于点 ,过点A作
,过点A作 轴于点
轴于点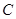 .
.
 的坐标.
的坐标. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF.
相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | A | B |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 .某经销商每天都要用汽车或火车将
.某经销商每天都要用汽车或火车将
 保鲜品一次性由A地运往B地.受各种因素限制,下周只能采取用汽车和火车中的一种进行运输且需提前预定.现有货运收费项目及收费标准表、行驶路
保鲜品一次性由A地运往B地.受各种因素限制,下周只能采取用汽车和火车中的一种进行运输且需提前预定.现有货运收费项目及收费标准表、行驶路 /
/
 与行驶时间
与行驶时间 /s的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
/s的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:| 运输工具 | 运输费单价元/( · ·  ) ) | 冷藏费单价元/( ·h) ·h) | 固定费用元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |

 /h,火车的速度为
/h,火车的速度为 
 /h;
/h;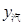 /元和
/元和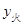 /元,分别求
/元,分别求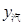 、
、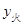 与
与 的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时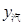 >
>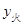 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com