
| | A | B |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
 =366
=366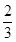
 =
=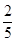 ;生产B种酒的利润率为
;生产B种酒的利润率为 =
=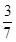 ,
,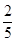 <
<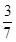 ,所以要使每天的利润率最大,应生产A种酒0瓶,B种酒700瓶.
,所以要使每天的利润率最大,应生产A种酒0瓶,B种酒700瓶.

科目:初中数学 来源:不详 题型:解答题
 的图象与反比例函数
的图象与反比例函数 的图象交于点A(1,m),与x轴交于点
的图象交于点A(1,m),与x轴交于点 ,过点A作
,过点A作 轴于点
轴于点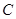 .
.
 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象如图所示.
的图象如图所示.
 ,求二次函数的解析式;
,求二次函数的解析式; ,点
,点 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 的图象于点N.若只有当1<m<
的图象于点N.若只有当1<m< 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式; 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出 的最大值.
的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 米,某天小敏从家里出发骑自行车上学,开始她以每分钟
米,某天小敏从家里出发骑自行车上学,开始她以每分钟 米的速度匀速行驶了
米的速度匀速行驶了 米,遇到交通堵塞,耽搁了
米,遇到交通堵塞,耽搁了 分钟,然后以每分钟
分钟,然后以每分钟 米的速度匀速前进一直到学校
米的速度匀速前进一直到学校 ,你认为小敏离家的距离
,你认为小敏离家的距离 与时间
与时间 之间的函数图象大致是( )
之间的函数图象大致是( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 轴上方作矩形
轴上方作矩形 ,且
,且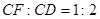 .设矩形
.设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.
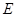 、
、 的坐标;
的坐标; 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式; 上存在点
上存在点 ,使
,使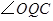 等于
等于 ,请直接写出
,请直接写出 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com