
【题目】如图1,在矩形![]() 中,
中,![]() 是
是![]() 的中点,以点
的中点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边EF、EG分别过点B、C.
的两边EF、EG分别过点B、C.


(1)求证:![]() ;
;
(2)将![]() 绕点
绕点![]() 按顺时针方向旋转,当旋转到
按顺时针方向旋转,当旋转到![]() 与
与![]() 重合时停止转动,若
重合时停止转动,若![]() 分别与
分别与![]() 相交于点
相交于点![]() (如图2).若
(如图2).若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)证明见解析;(2)△BMN面积的最大值为2.
【解析】
(1)由中点的定义可得AE=ED,根据矩形的性质可得AB=CD,∠BAE=∠CDE,利用SAS可证明△BAE≌△CDE,即可证明BE=CE;
(2)由(1)可知BE=CE,可得△BEC是等腰直角三角形,可得∠EBC=45°,根据矩形的性质可得∠ABE=45°,可证明△ABE是等腰直角三角形,可得AB=AE,由E为AD中点可得AD=2AB=4,根据矩形的性质可得BC的长,根据旋转的性质可得∠BEM=∠CEN,利用ASA可证明△BEM≌△CEN,可得BM=CN,设BM=x,则BN=4-x,根据三角形面积公式可得S△BMN=![]() x(4-x)=-
x(4-x)=-![]() (x-2)2+2,利用平方的非负数性质即可得答案.
(x-2)2+2,利用平方的非负数性质即可得答案.
(1)∵点E为AD中点,
∴AE=DE,
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D=90°,
在△BAE和△CDE中, ,
,
∴△BAE≌△CDE,
∴BE=CE.
(2)∵BE=CE,∠BEC=90°,
∴△BEC是等腰直角三角形,
∴∠EBC=45°,
∴∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AB=AE,
∵点E为AD中点,AB=2,
∴AD=BC=2AB=4,
∵将![]() 绕点
绕点![]() 按顺时针方向旋转,
按顺时针方向旋转,
∴∠BEM=∠CEN,
在△BEM和△CEN中, ,
,
∴△BEM≌△CEN,
∴BM=CN,
设MB=x,则BN=BC-CN=4-x,
∴S△BMN=![]() BN·BM=
BN·BM=![]() x(4-x)=-
x(4-x)=-![]() (x-2)2+2,
(x-2)2+2,
∵(x-2)2≥0,
∴-![]() (x-2)2+2≤2,
(x-2)2+2≤2,
∴△BMN面积的最大值为2.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF= ![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当S△PAB=S△OAB , 求△PAB周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料I:
教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则:
的两根,则:![]() __ _,
__ _,![]() __ _,那么_
__ _,那么_![]() (请你完成以上的填空)
(请你完成以上的填空)
阅读材料:II
已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)若![]() 且
且![]() 则
则![]() ;
;
(3)已知![]() 且
且![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,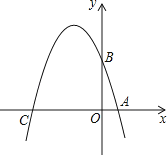
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6).
(1)求二次函数的解析式;
(2)画出它的图象;
(3)写出它的对称轴和顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com