
【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O. 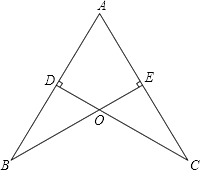
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明.
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为![]() .
.
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在抛物线y=x2-2x-1上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
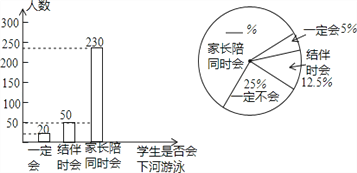
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 名学生;
(2)“家长陪同时会”的学生所占比例为 %,“一定不会”的学生有 人;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.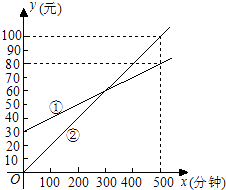
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和爸爸一起玩投篮球游戏,两人商定规则为:小丽投中1个得3分,爸爸投中1个得1分,结果两人一共投中了20个,得分刚好相等.小丽投中了_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC,BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC和△DCF面积的关系是______________;(请在横线上填写“相等”或“不等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI,正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.
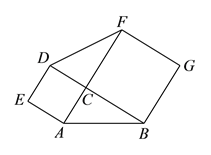
图1
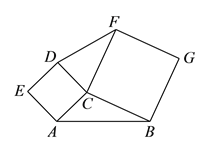
图2
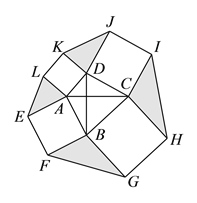
图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com