
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
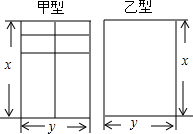 如图所示,是两种长方形塑钢窗框,已知窗框的长都是x米,窗框的宽都是y米,若一用户装修房屋,需要甲型窗框5个,乙型窗框3个,求共需要塑钢多少米(用含x、y的代数式表示).
如图所示,是两种长方形塑钢窗框,已知窗框的长都是x米,窗框的宽都是y米,若一用户装修房屋,需要甲型窗框5个,乙型窗框3个,求共需要塑钢多少米(用含x、y的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边△ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=1,则EF的长为$\sqrt{3}$.
如图,在等边△ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=1,则EF的长为$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com