
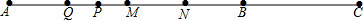
分析 根据线段中点的性质,可得AQ=QM=$\frac{AM}{2}$=$\frac{AB}{4}$,AP=NP=$\frac{AN}{2}$=$\frac{AC}{4}$,根据线段的和差,可得MN,PQ,根据比的性质,可得答案.
解答 解:如图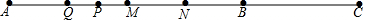 ,
,
∵M是AB的中点,
∴AM=BM=$\frac{AB}{2}$.
∵Q是MA的中点,
∴AQ=QM=$\frac{AM}{2}$=$\frac{AB}{4}$.
∵N是AC的中点,
∴AN=CN=$\frac{AC}{2}$.
∵P是NA的中点,
∴AP=NP=$\frac{AN}{2}$=$\frac{AC}{4}$,
∴MN=AN-AM=$\frac{AC}{2}$-$\frac{AB}{2}$=$\frac{AC-AB}{2}$,
PQ=AP-AQ=$\frac{AC}{4}$-$\frac{AB}{4}$=$\frac{AC-AB}{4}$,
∴MN:PQ=$\frac{AC-AB}{2}$:$\frac{AC-AB}{4}$=2:1.
点评 本题考查了两点间的距离,利用线段中点的性质、线段的和差得出MN,PQ是解题关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
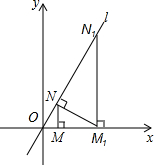 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±1 | B. | 1 | C. | -1 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com