
分析 题目应该先化简再求值,分式得先约分,结果需化简.
解答 解:(1)原式=$\frac{(a-{a}^{-1})^{2}}{(a+{a}^{-1})(a-{a}^{-1})}$+$\root{6}{{b}^{4}}$=$\frac{a-{a}^{-1}}{a+{a}^{-1}}$+$\root{6}{{b}^{4}}$=$\frac{{a}^{2}-1}{{a}^{2}+1}$+${b}^{\frac{2}{3}}$,
当a=4,b=27时,原式=$\frac{15}{17}$+[(3)3]${\;}^{\frac{2}{3}}$=$\frac{15}{17}+9=9\frac{15}{17}$;
(2)原式=$\frac{{a}^{\frac{1}{2}}×{b}^{\frac{1}{2}}}{{b}^{\frac{-1}{2}}×{a}^{\frac{-2}{3}}}$÷$\frac{{a}^{\frac{2}{3}}×{b}^{\frac{1}{3}}}{{b}^{-\frac{2}{3}}×{a}^{\frac{-1}{3}}}$=${a}^{(\frac{1}{2}+\frac{2}{3})}$${b}^{(\frac{1}{2}+\frac{1}{2})}$÷${a}^{(\frac{2}{3}+\frac{1}{3})}{b}^{(\frac{1}{3}+\frac{2}{3})}$=${a}^{\frac{7}{6}}b÷ab={a}^{\frac{1}{6}}$=4${\;}^{\frac{1}{6}}$=$\root{3}{2}$.
点评 此题考查了约分、负整数指数幂、完全平方公式、平方差公式、幂的相关运算及实数的运算,熟记公式,正确的利用运算法则是解本题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.
如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
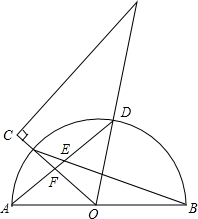 如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.
如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com