
����Ŀ����ͼ1��������ȫ�ȵ����ǰ�ABC��EFG������һ��ʹ���ǰ�EFG��ֱ�DZ�FG�������ǰ�ABC��ֱ�Ƕ���C����ֱAB��G�����С�B=��F=30����б��AB��EF��Ϊ4���ֽ����ǰ�EFG��ͼ1��ʾ��λ����G������ʱ�뷽����ת![]() ��0��
��0��![]() ��90��������ͼ2��EG��AC�ڵ�K��GF��BC�ڵ�H������ת�����У��������������⣺
��90��������ͼ2��EG��AC�ڵ�K��GF��BC�ڵ�H������ת�����У��������������⣺
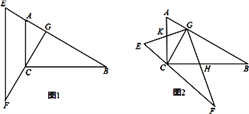
��1����֤����CGH�ס�AGK��
��2������HK����֤��KH��EF��
��3����AK=x����CKH�����Ϊy����y����x�ĺ�����ϵʽ�������y�����ֵ��
���𰸡���1��֤��������;��2��֤��������;��3��y= ![]() , y���ֵΪ
, y���ֵΪ![]() .
.
�������������������1��GH��GK��ֵû�����仯��������֪����֤����AGK�ס�CGH�������������ε����ʿɵã� ![]() =
=![]() ������Ϊ��Rt��ACG�У�tan��A=
������Ϊ��Rt��ACG�У�tan��A=![]() =
=![]() ������GH��GK�ı�ֵ��һ����ֵ
������GH��GK�ı�ֵ��һ����ֵ![]() ��
��
��2������HK���ɣ�1����֪��Rt��KHG�У�tan��GKH=![]() =
=![]() �����ԡ�GKH=60�����ٸ��������ε��ڽǺ�֤������E=��EGF-��F=90��-30��=60��������֤�á�GKH=��E=60��������ͬλ���������ƽ�м���֤��KH��EF��
�����ԡ�GKH=60�����ٸ��������ε��ڽǺ�֤������E=��EGF-��F=90��-30��=60��������֤�á�GKH=��E=60��������ͬλ���������ƽ�м���֤��KH��EF��
��3����AK=x������x=1��ʹ��CKH���������ɣ�1������AGK�ס�CGH������CH=![]() AK=
AK=![]() x�����������ε������ʽ��ʾ��S��CHK=
x�����������ε������ʽ��ʾ��S��CHK=![]() CKCH=
CKCH=![]() ��2-x��
��2-x��![]() x���ٰѶ��κ����Ľ���ʽ��Ϊ����ʽ�������x��ֵ��
x���ٰѶ��κ����Ľ���ʽ��Ϊ����ʽ�������x��ֵ��
���������
��1��֤������Rt��ABC�У�CG��AB����B=30����
���GCH=��GAK=60��.
�֡�CGH=��AGK= ![]() ��
��
���CGH�ס�AGK.
��2��֤��������HK��

�ɣ�1������CGH�ס�AGK��
��![]() .
.
��Rt��ACG��tanA=![]() =
=![]() ��
��
��![]() .
.
��Rt��KHG��tan��GKH=![]() ��
��
���GKH=60��.
��Rt��EFG����F=30�������E=60����
���GKH=��E��
��KH��EF.
��3���⣺�ɣ�1������CGH�ס�AGK��
��![]()
�ɣ�2��֪![]() ����
����![]() .
.
��CH=![]() AK=
AK= ![]() .
.
��Rt��ABC����B=30����
��AC=![]() AB=2��
AB=2��
��CK=AC-AK=2-x.
��y=![]() CK��CH=
CK��CH= ![]() =
= ![]() .
.
��y=![]() .
.
�൱x=1ʱ��y�����ֵΪ![]() .
.
�㾦: ���⿼��������������ε��ж������ʼ�ͼ����ת�����ʡ�ƽ���ߵ��ж������ʡ������ε������ʽ�����κ�������ֵ���⣬��Ŀ���ۺ��Ժ�ǿ���Ѷ��еȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
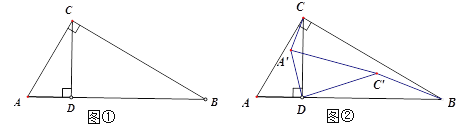
����Ŀ����ͼ�٣���Rt��ABC�У���C=90��, ��B=30��,AC=1,CD��AB������ΪD���ֽ���ACD��D��˳ʱ����ת![]() �õ���A��C��D, ��תʱ��Ϊt�룬��ACD��D����ת�Ľ��ٶ�
�õ���A��C��D, ��תʱ��Ϊt�룬��ACD��D����ת�Ľ��ٶ�![]() /��(ÿ��ת10��) ��
/��(ÿ��ת10��) ��
��1����תʱ��t= ��ʱ��A��C����AB;
��2����ACD��D��˳ʱ����תһ�ܣ�3600����б��ACɨ�������Ϊ ��
��3����ͼ�ڣ�����A��C�� C��B��
����6��t��9����֤�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
�ڵ�t��9ʱ���������ۻ������������ֱ��д����ֵ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=![]() x�뷴��������y=
x�뷴��������y=![]() ��k��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��k��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ4��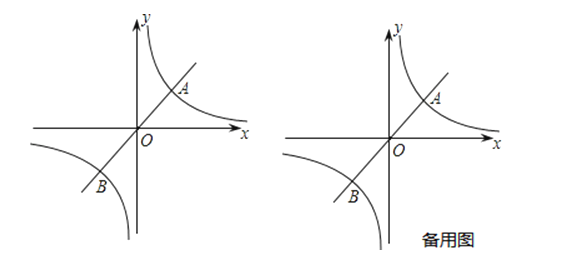
��1����k��ֵ��
��2������ͼ��ֱ��д������������ֵС�ڷ���������ֵʱx��ȡֵ��Χ��
��3����ԭ��O����һ��ֱ��l��˫����y=![]() ��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ�A��P��B��QΪ������ɵ��ı������Ϊ24�����P�����꣮
��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ�A��P��B��QΪ������ɵ��ı������Ϊ24�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+2��x�ᡢy��ֱ��ڵ�A(-1,0)�͵�B���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
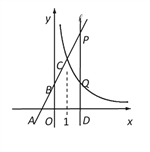
��1����k��ֵ��
��2�����������Ľ���ʽ��
��3����x���ϵĵ�D��a��0����ƽ����y���ֱ��![]() ��a��1�����ֱ���ֱ��AB��˫����
��a��1�����ֱ���ֱ��AB��˫����![]() ���ڵ�P��Q����PQ=2QD�����D�����꣮
���ڵ�P��Q����PQ=2QD�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ڴ�����3����С��ͬ��С�������Ϸֱ�д������1��2��3���Ӵ������������һ��С��¼�����ֺ�Żأ������������һ��С��
��1����������ͼ���б����е�һ�֣��оٳ������������������ֵ����п��ܽ����
��2�����������������ϵ����ֺ�Ϊż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
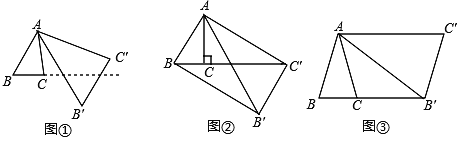
����Ŀ������ABC�Ƶ�A����ʱ�뷽����ת���ȣ���ʹ���߳���Ϊԭ����n�����á�AB��C�� ����ͼ����ʾ����BAB�� ������ ![]() �����ǽ����ֱ任��Ϊ[����n] ��
�����ǽ����ֱ任��Ϊ[����n] ��
��1����ͼ�٣��ԡ�ABC���任[60����![]() ]�õ���AB��C�� ����
]�õ���AB��C�� ����![]() :
:![]() = ��ֱ��BC��ֱ��B��C�����е����Ϊ �ȣ�
= ��ֱ��BC��ֱ��B��C�����е����Ϊ �ȣ�
��2����ͼ������ABC�У���BAC=30������ACB=90�����ԡ�ABC���任[����n]�õ���AB��C����ʹ��B��C��![]() ��ͬһֱ���ϣ����ı���ABB��C��Ϊ���Σ�������n��ֵ��
��ͬһֱ���ϣ����ı���ABB��C��Ϊ���Σ�������n��ֵ��
��3����ͼ������ABC�У�AB=AC����BAC=36����BC=1���ԡ�ABC���任[����n]�õ���AB��C����ʹ��B��C��B����ͬһֱ���ϣ����ı���ABB��C��Ϊƽ���ı��Σ�������n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽx5y2+2x4y3��3x2y2��4xy�ǣ�������
A.��x����������
B.��x�Ľ�������
C.��y����������
D.��y�Ľ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
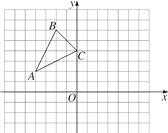
����Ŀ����ͼ����֪A(��4��2)��B(��2��6)��C(0��4)��ֱ������ϵ�е����㣮
(1)�ѡ�ABC����ƽ��4����λ������ƽ��1����λ���õ���A1B1C1������ƽ�ƺ��ͼ�Σ���д����A�Ķ�Ӧ��A1�����ꣻ
(2)��ԭ��OΪλ�����ģ�����ABC��СΪԭ����һ�룬�õ���A2B2C2����������������ϵ��������������������ͼ�Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com