
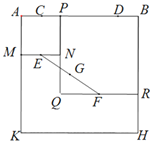
【题目】如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
【答案】2.
【解析】
试题设KH的中点为S,连接PE、SE、SF、PS,由三角形相似,结合E为MN的中点,S为KH的中点可得A、E、S共线,F为QR的中点,S为KH 的中点得B、F、S共线,再由三角形相似得到:ES∥PF,PE∥FS,结合G为EF的中点,可得G为PS的中点,即G的移动路线为△CSD的中位线,由三角形的中位线长是底的一半得答案.
试题解析:如图,
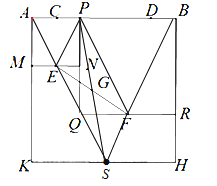
设KH的中点为S,连接PE、SE、SF、PS,
∵E为MN的中点,S为KH的中点
∴A、E、S共线
∵F为QR的中点,S为KH 的中点
∴B、F、S共线
由△AME∽△PQF,得∠SAP=∠FPB
∴ES∥PF
由△PNE∽△BRF,得∠EPA=∠FBP
∴PE∥FS
则四边形PESF为平行四边形,则G为PS的中点
∴点G移动路径为△CSD的中位线,
∵CD=AB-AC-BD=6-1-1=4
∴点G移动路径长为![]() ×4=2.
×4=2.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,对称轴是直线x=﹣1,点B的坐标为(1,0).下面的四个结论:①AB=4;②b2﹣4ac>0;③ab<0;④a﹣b+c<0,其中正确的结论是_____(填写序号).
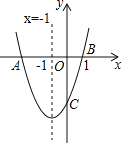
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都完全相同的四张卡片A、B、C、D,正面上分别写有四个实数![]() 、
、![]() 、
、![]() 、
、![]() ,将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
,将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)用画树形图或列表法表示抽取两张卡片可能出现的所有情况卡片(可用A、B、C、D表示);
(2)求抽到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
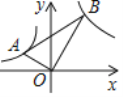
【题目】在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,若sin∠BAO =
(x>0)的图象上,若sin∠BAO = ![]() ,则k的值为__________.
,则k的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有四个小球,上面分别标有数字﹣2,﹣1,0,1,它们除了数字不同外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是 .
(2)小聪先从袋子中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标;然后放回搅匀,接着小明从袋子中随机摸出一个小球,记下数字作为点M的纵坐标.如图,已知四边形ABCD的四个顶点的坐标分别为A(﹣2,0),B(0,﹣2),C(1,0),D(0,1),请用画树状图或列表法,求点M落在四边形ABCD所围成的部分内(含边界)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分,为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
D等 | 60<x≤70 | 5 |
C等 | 70<x≤80 | a |
B等 | 80<x≤90 | b |
A等 | 90<x≤100 | 2 |
九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 | c | m% |
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:a= ,c= ,m= ;
(2)八年级小宇和九年级小乐的分数都为80分,请判断小宇、小乐在各自年级的排名哪位更靠前?请简述你的理由;
(3)若九年级共有600人参加参赛,请估计九年级80分以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图11,一转盘被等分成三个扇形,上面分别标有关-1,1,
2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,鞭个扇形恰好停在指针所
指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
⑴若小静转动转盘一次,求得到负数的概率;
⑵小宇和小静分别转动一次,若两人得到的数相同,则称两人“不谋而合”,用列表法(或画树形图)求两人“不谋而合”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com