
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,对称轴是直线x=﹣1,点B的坐标为(1,0).下面的四个结论:①AB=4;②b2﹣4ac>0;③ab<0;④a﹣b+c<0,其中正确的结论是_____(填写序号).
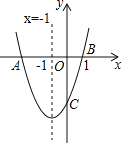
科目:初中数学 来源: 题型:
【题目】某校共抽取50名同学参加学校举办的“预防新冠肺炎”知识测验,所得成绩分别记作60分、70分、80分、90分、100分,并将统计结果绘制成不完整的扇形统计图(如图).
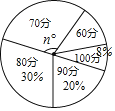
(1)若n=108,则成绩为60分的人数为 ;
(2)若从这50位同学中,随机抽取一人,求抽到同学的分数不低于90分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
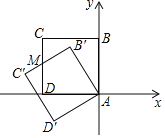
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
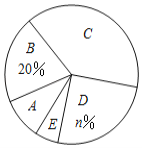
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
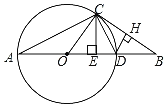
【题目】如图,O是![]() ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
(1)求证:直线BC是⊙O的切线;
(2)若⊙O的半径为3,CD=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好新冠肺炎疫情期间开学工作,我区某中学用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
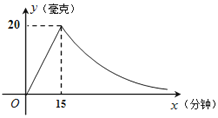
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ABC内接于⊙O,AB=AC,
ABC内接于⊙O,AB=AC,![]() .过点A作AD//BC,与
.过点A作AD//BC,与![]() 的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
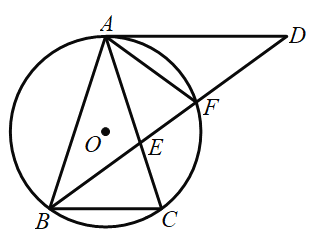
(1)求证:AD是⊙O的切线
(2)求证:![]()
(3)若BC=2,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
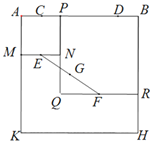
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com