
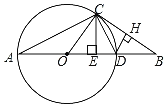
【题目】如图,O是![]() ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
(1)求证:直线BC是⊙O的切线;
(2)若⊙O的半径为3,CD=2,求BC的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明∠OCD+∠DCB=90°,得出∠OCB=90°,则结论得证;
(2)证明△CDB∽△ACB,得出![]() ,设BC=x,则AB=2
,设BC=x,则AB=2![]() x,DB=2
x,DB=2![]() x﹣6,由BC2=ABDB得出方程,解方程则可得出答案.
x﹣6,由BC2=ABDB得出方程,解方程则可得出答案.
(1)证明:∵CE⊥AB,
∴∠CED=90°,
∴∠ECD+∠CDE=90°,
∵OC=DO,
∴∠ODC=∠OCD,
∵CD平分∠BCE,
∴∠ECD=∠DCB,
∴∠OCD+∠DCB=90°,
∴∠OCB=90°,
∴直线BC是⊙O的切线;
(2)∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠CDA=90°,
∵∠DCB+∠ODC=90°,
∴∠DCB=∠CAD,
∵∠CBD=∠ABC,
∴△CDB∽△ACB,
∴![]() ,
,
∴BC2=ABDB
∵⊙O的半径为3,CD=2,
∴AC=![]() =
=![]() =4
=4![]() ,
,
∴![]() =
=![]() ,
,
设BC=x,则AB=2![]() x,DB=2
x,DB=2![]() x﹣6,
x﹣6,
∴x2=2![]() ,
,
解得x=![]() ,
,
∴BC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们将抛物线![]() 通过平移后得到
通过平移后得到![]() ,且设平移后所得抛物线的顶点依次为
,且设平移后所得抛物线的顶点依次为![]() ,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
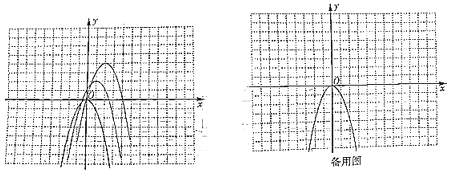
(1)![]() 的坐标为____________,直接写出平移后抛物线
的坐标为____________,直接写出平移后抛物线![]() 的解析式为____________(用k表示);
的解析式为____________(用k表示);
(2)若平移后的抛物线![]() 与抛物线
与抛物线![]() 交于点A,对称轴与抛物线
交于点A,对称轴与抛物线![]() 交于点B,若
交于点B,若![]() ,求整数k的值.
,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
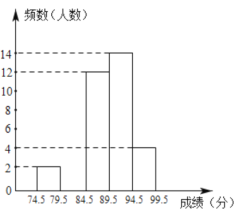
【题目】某校开展“祖国在我心中”主题演讲比赛,参加选拔比赛的选手的成绩(满分为![]() 分),分成五组,制成了如下不完整的统计图表.
分),分成五组,制成了如下不完整的统计图表.
分数段 | 频数 | 频率 |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
(1)求分数在![]() 参赛学生的频率;
参赛学生的频率;
(2)求分数在![]() 参赛学生的频数,并补全频数分布直方图;
参赛学生的频数,并补全频数分布直方图;
(3)成绩在![]() 分以上的选手中,有三名男生和一名女生,学校从中随机确定
分以上的选手中,有三名男生和一名女生,学校从中随机确定![]() 名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
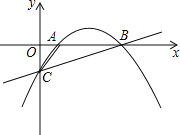
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,对称轴是直线x=﹣1,点B的坐标为(1,0).下面的四个结论:①AB=4;②b2﹣4ac>0;③ab<0;④a﹣b+c<0,其中正确的结论是_____(填写序号).
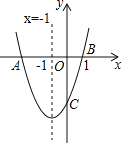
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情发生后,口罩市场出现热销,小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售,销售完后共获利2700元,进价和售价如下表:
品名价格 | 医用外科口罩 | N95口罩 |
进价(元/袋) | 20 | 30 |
售价(元/袋) | 25 | 36 |
(1)小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋?
(2)该药房第二次以原价购进医用外科、N95两种型号口罩,购进医用外科口罩袋数不变,而购进N95口罩袋数是第一次的2倍,医用外科口罩按原售价出售,而效果更好的N95口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋N95口罩最多打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() .
.
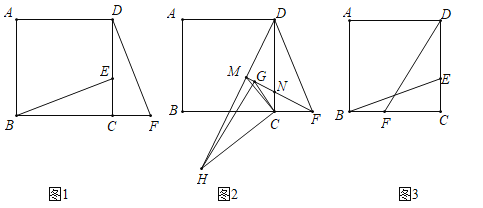
(1)如图1,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
①求证:![]() ;
;
②如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到对应
得到对应![]() ,射线
,射线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
(2)如图3,若![]() ,点
,点![]() 是
是![]() 边上的动点,且
边上的动点,且![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com