
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() .
.
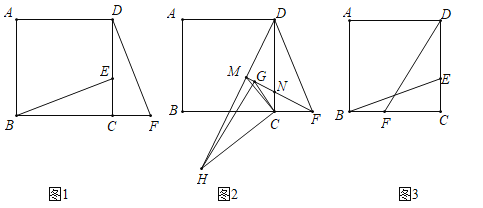
(1)如图1,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
①求证:![]() ;
;
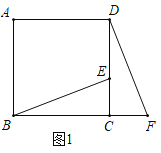
②如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到对应
得到对应![]() ,射线
,射线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
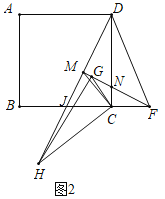
(2)如图3,若![]() ,点
,点![]() 是
是![]() 边上的动点,且
边上的动点,且![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)①详见解析;②详见解析;(2)![]()
【解析】
(1)①欲证明DF=BE,只要证明△BCE≌△DCF(SAS)即可.
②证明△DCJ∽△FMJ,推出![]() ,推出△JMC∽△JFD,可得
,推出△JMC∽△JFD,可得![]() ,推出DF=2CM可得结论.
,推出DF=2CM可得结论.
(2)如图3中,连接AE,延长BC到T,使得CT=BC,连接AT.想办法证明DF=AE,BE=ET,推出DF+BE=AE+ET.根据AE+ET≥AT,利用勾股定理求出AT即可解决问题.
(1)①证明:如图1中,
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
∵CE=CF,
∴△BCE≌△DCF(SAS),
∴BE=DF.
②解:结论:HG=2CM.
理由:如图2中,设DH交BC于J.
∵∠DCG=30°,∠DCF=90°,
∴∠GCF=120°,
∵CG=CF,
∴∠CFG=∠CGF=30°,
∵CD=CH,∠DCH=120°,
∴∠CDH=∠CHD=30°,
∵∠DCJ=90°,
∴∠DJC=60°,DJ=2CJ
∴∠JMF=90°,
∵∠DJC=∠FJM,∠DCJ=∠FMJ,
∴△DCJ∽△FMJ,
∴![]() ,
,
∵∠MJC=∠FJD,
∴△JMC∽△JFD,
∴![]() ,
,
∴DF=2CM,
∵HG=DF,
∴HG=2CM.
(2)如图3中,连接AE,延长BC到T,使得CT=BC,连接AT.
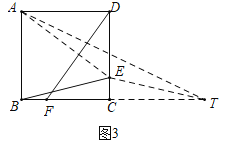
∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠DCF=∠ABT=90°,
∵CF+CE=2=CD=CE+DE,
∴DE=CF,
∴△ADE≌△DCF(SAS),
∴AE=DF,
∵CD⊥BT,CB=CT,
∴EB=ET,
∴DF+BE=AE+ET,
∵AE+ET≥AT,AT=![]() ,
,
∴DF+BE=AE+ET≥![]() ,
,
∴DF+BE的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
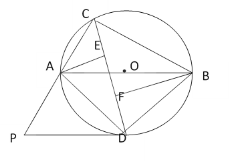
(1)求证:DP∥AB;
(2)试猜想线段AE、EF、BF之间的数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
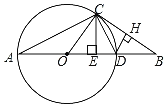
【题目】如图,O是![]() ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
ABC的边AB上一点,⊙O经过点A、C,交AB于点D.过点C作CE⊥AB,垂足为E.连接CD,CD恰好平分∠BCE.
(1)求证:直线BC是⊙O的切线;
(2)若⊙O的半径为3,CD=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ABC内接于⊙O,AB=AC,
ABC内接于⊙O,AB=AC,![]() .过点A作AD//BC,与
.过点A作AD//BC,与![]() 的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
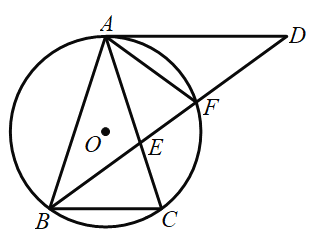
(1)求证:AD是⊙O的切线
(2)求证:![]()
(3)若BC=2,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
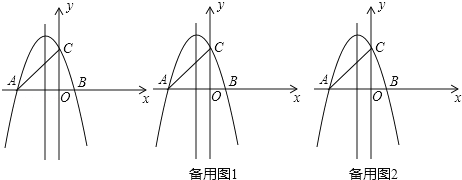
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com