
已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
【考点】根的判别式;解一元二次方程-因式分解法;三角形三边关系;等腰三角形的性质.
【专题】计算题;压轴题.
【分析】(1)先计算出△=1,然后根据判别式的意义即可得到结论;
(2)先利用公式法求出方程的解为x1=k,x2=k+1,然后分类讨论:AB=k,AC=k+1,当AB=BC或AC=BC时△ABC为等腰三角形,然后求出k的值.
【解答】(1)证明:∵△=(2k+1)2﹣4(k2+k)=1>0,
∴方程有两个不相等的实数根;
(2)解:一元二次方程x2﹣(2k+1)x+k2+k=0的解为x=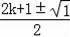
 ,即x1=k,x2=k+1,
,即x1=k,x2=k+1,
∵k<k+1,
∴AB≠AC.
当AB=k,AC=k+1,且AB=BC时,△ABC是等腰三角形,则k=5;
当AB=k,AC=k+1,且AC=BC时,△ABC是等腰三角形,则k+1=5,解得k=4,
综合上述,k的值为5或4.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了三角形三边的关系以及等腰三角形的性质.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论:
①4ac﹣b2<0;
②若点(x1,y1)在抛物线上,且x1≠﹣1,则有a﹣ax12>bx1+b;
③a+b+c<0;
④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,
其中正确结论的个数是( )
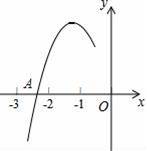

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
某市为缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).
(1)求调整后楼梯AD的长;
(2)求BD的长.
(结果保留根号)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com