
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x-1 | |||||||
| -3x | |||||||
| x2 |
分析 根据题意计算,填写表格即可;
(1)从表格中找出使代数式2x-1的值为5时x的值即可;
(2)根据表格找出使代数式-3x和x2的值相等x的值即可;
(3)观察表格中的数据,找出随着x的值的逐渐增大,代数式2x-1、-3x和x2的值变化趋势.
解答 解:填表如下:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x-1 | -7 | -5 | -3 | -1 | 1 | 3 | 5 |
| -3x | 9 | 6 | 3 | 0 | -3 | -6 | -9 |
| x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
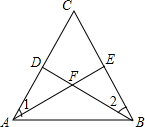 已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )
已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com