
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是①④(将正确的结论填在横线上).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是①④(将正确的结论填在横线上).分析 ①正确.由四边形ABCD是矩形,推出S△OBC=S△OBA,由点E、点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,推出S△CEO=S△OAD=$\frac{k}{2}$,即可推出S△OEB=S△OBD.
②错误.设点B(m,n),D(m,n′)则M($\frac{1}{2}$m,$\frac{1}{2}$n,),由点M,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,可得$\frac{1}{2}$m•$\frac{1}{2}$n=m•n′,推出n′=$\frac{1}{4}$n,推出AD=$\frac{1}{4}$AB,推出BD=3AD,故②错误.
③错误.因为S△ODM=S△OBD-S△BDM=$\frac{1}{2}$•$\frac{3}{4}$b•a-$\frac{1}{2}$•$\frac{3}{4}$b•$\frac{1}{2}$a=$\frac{3}{16}$ab,S△CEO=S△OAD=$\frac{1}{2}$•a•$\frac{1}{4}$b=$\frac{1}{8}$ab,所以S△ODM:S△OCE=$\frac{3}{16}$ab:$\frac{1}{8}$ab=3:2,故③错误.
④正确.由$\frac{BE}{EC}$=$\frac{BD}{AD}$=3,推出DE∥AC,推出△BED∽△BCA.
解答 解:∵四边形ABCD是矩形,
∴S△OBC=S△OBA,
∵点E、点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴S△CEO=S△OAD=$\frac{k}{2}$,
∴S△OEB=S△OBD,故①正确,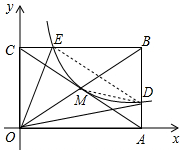
设点B(m,n),D(m,n′)则M($\frac{1}{2}$m,$\frac{1}{2}$n,),
∵点M,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴$\frac{1}{2}$m•$\frac{1}{2}$n=m•n′,
∴n′=$\frac{1}{4}$n,
∴AD=$\frac{1}{4}$AB,
∴BD=3AD,故②错误,
连接DM,∵S△ODM=S△OBD-S△BDM=$\frac{1}{2}$•$\frac{3}{4}$b•a-$\frac{1}{2}$•$\frac{3}{4}$b•$\frac{1}{2}$a=$\frac{3}{16}$ab,
∵S△CEO=S△OAD=$\frac{1}{2}$•a•$\frac{1}{4}$b=$\frac{1}{8}$ab,
∴S△ODM:S△OCE=$\frac{3}{16}$ab:$\frac{1}{8}$ab=3:2,故③错误,
连接DE,同法可证CE=$\frac{1}{4}$BC,
∴BE=3EC,
∴$\frac{BE}{EC}$=$\frac{BD}{AD}$=3,
∴DE∥AC,
∴△BED∽△BCA,故④正确.
故答案为①④
点评 本题考查反比例函数综合题、矩形的性质、三角形的面积、中点坐标公式等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,学会用分割法求三角形面积,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
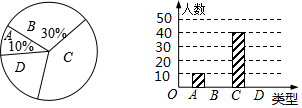 某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.
某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com