
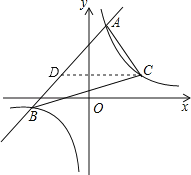
【题目】已知一次函数y1=x+m的图象与反比例函数![]() 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.

(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
【答案】(1)y1=x+5 (2)21
【解析】
试题分析:(1)首先根据x>1时,y1>y2,0<x<1时,y1<y2确定点A的横坐标,然后代入反比例函数解析式求出点A的纵坐标,从而得到点A的坐标,再利用待定系数法求直线解析式解答;
(2)根据点C到y轴的距离判断出点C的横坐标,代入反比例函数解析式求出纵坐标,从而得到点C的坐标,过点C作CD∥x轴交直线AB于D,求出点D的坐标,然后得到CD的长度,再联立一次函数与双曲线解析式求出点B的坐标,然后△ABC的面积=△ACD的面积+△BCD的面积,列式进行计算即可得解.
解:(1)∵当x>1时,y1>y2;当0<x<1时,y1<y2,
∴点A的横坐标为1,
代入反比例函数解析式,![]() =y,
=y,
解得y=6,
∴点A的坐标为(1,6),
又∵点A在一次函数图象上,
∴1+m=6,
解得m=5,
∴一次函数的解析式为y1=x+5;
(2)∵第一象限内点C到y轴的距离为3,
∴点C的横坐标为3,
∴y=![]() =2,
=2,
∴点C的坐标为(3,2),
过点C作CD∥x轴交直线AB于D,
则点D的纵坐标为2,
∴x+5=2,
解得x=﹣3,
∴点D的坐标为(﹣3,2),
∴CD=3﹣(﹣3)=3+3=6,
点A到CD的距离为6﹣2=4,
联立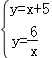 ,
,
解得![]() (舍去),
(舍去),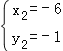 ,
,
∴点B的坐标为(﹣6,﹣1),
∴点B到CD的距离为2﹣(﹣1)=2+1=3,
S△ABC=S△ACD+S△BCD=![]() ×6×4+
×6×4+![]() ×6×3=12+9=21.
×6×3=12+9=21.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(一6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.

(1)直接写出线段BO的长:
(2)求点D的坐标;
(3)若点N是平面内任一点,在x轴上是否存在点M,使咀M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.
(1)如图1,当有2个电子元件![]() 并联时,请你用树状图表示图中
并联时,请你用树状图表示图中![]() 之间电流能否通过的所有可能情况,并求出
之间电流能否通过的所有可能情况,并求出![]() 之间电流通过的概率;
之间电流通过的概率;
(2)如图2,当有3个电子元件并联时,求![]() 之间电流通过的概率.
之间电流通过的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在![]() 中,分别以
中,分别以![]() 、
、![]() 为斜边,向
为斜边,向![]() 的形外作等腰直角三角形,直角的顶点分别为
的形外作等腰直角三角形,直角的顶点分别为![]() ,点
,点![]() 分别为
分别为![]() 边的中点.问:
边的中点.问: ![]() 是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);
(2)如图2,在![]() 中,分别以
中,分别以![]() 为底边,向
为底边,向![]() 的形外作等腰三角形,顶角的顶点分别为
的形外作等腰三角形,顶角的顶点分别为![]() ,且
,且![]() .点
.点![]() 分别为
分别为![]()
![]() 边的中点.
边的中点.
①试判断![]() 是否满足(1)中的关系?若满足,请说明理由;若不满足,请写
是否满足(1)中的关系?若满足,请说明理由;若不满足,请写![]() 之间存在的一种关系,并加以说明.
之间存在的一种关系,并加以说明.
②若![]() ,
, ![]() ,
, ![]() 的面积为32,求
的面积为32,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试,并以同一标准分成“不合格”、“合格”、“优秀”3个等级,为了解培训效果,用抽样调查的方式从中抽取32名学生的2次测试等级,并绘制成条形统计图:

(1)这32名学生经过培训,测试等级“不合格”的百分比比培训前减少了多少?
(2)估计该校八年级学生中,培训前、后等级为“合格”与“优秀”的学生各有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图像反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图像回答下列问题:

(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点,且∠DBC=∠BAC, ![]() .
.
(1) 求证:BD是⊙O的切线;
(2) 求![]() 的值;
的值;
(3) 如图2,过点B作BG⊥AC交AC于点F,交⊙O于点G,BC、AG的延长线交于点E,⊙O的半径为6,求BE的长.
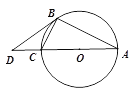
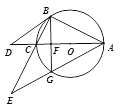
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水![]() 与滴水时间
与滴水时间![]() 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图![]() 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图![]() 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.
(![]() )容器内原有水多少升.
)容器内原有水多少升.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com