
【题目】如图1,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点,且∠DBC=∠BAC, ![]() .
.
(1) 求证:BD是⊙O的切线;
(2) 求![]() 的值;
的值;
(3) 如图2,过点B作BG⊥AC交AC于点F,交⊙O于点G,BC、AG的延长线交于点E,⊙O的半径为6,求BE的长.
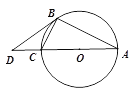
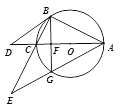
图1 图2
【答案】(1)见解析; (2) ![]() ;(3)
;(3) ![]()
![]()
【解析】试题分析:(1)连接OB.欲证明![]() 是切线,只要证明
是切线,只要证明![]() 即可;
即可;
(2)由△DBC∽△DAB,推出![]() 在Rt△ABC中,
在Rt△ABC中, ![]() 推出
推出![]() 设CD=a,则BD=2a,AD=4a,AC=3a,由此即可解决问题;
设CD=a,则BD=2a,AD=4a,AC=3a,由此即可解决问题;
(3)如图2中,连接CG.由△ECG∽△EAB,推出![]() ,设EC=y,则
,设EC=y,则![]() 由此想办法列出方程即可解决问题;
由此想办法列出方程即可解决问题;
试题解析:(1)证明:如图1中,连接OB.
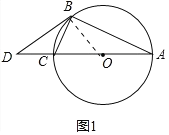
∵AB是直径,
∴![]()
∵OB=OA=OC,
∴∠A=∠OBA,∠OBC=∠OCB,
![]()
![]()
∴![]() 即OB⊥BD,
即OB⊥BD,
∴DB是⊙O的切线.
(2)∵∠D=∠D,∠DBC=∠A,
∴△DBC∽△DAB,
![]()
在Rt△ABC中, ![]()
![]() 设CD=a,则BD=2a,AD=4a,AC=3a,
设CD=a,则BD=2a,AD=4a,AC=3a,
![]()
![]()
(3)如图2中,连接CG.

在Rt△ABC中,∵AC=12,BC:AB=1:2,
∴![]()
∵AC⊥BG,
∴BF=FG,
![]() BC=CG,
BC=CG,
∵∠E=∠E,∠ECG=∠EAB,
∴△ECG∽△EAB,
∴![]() ,设EC=y,则
,设EC=y,则![]()
∵BE=2EG,
∴![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=x+m的图象与反比例函数![]() 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.

(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全面提高学生的能力,学校组织课外活动小组,并要求初一学年积极参加,初一学年共有四个班,参加的学生共有(6a﹣3b)人,其中一班有a人参加,二班参加的人数比一班参加的人数两倍少b人,三班参加的人数比二班参加的人数一半多1人.
(1)求三班的人数(用含a,b的式子表示);
(2)求四班的人数(用含a,b的式子表示);
(3)若四个班共54人参加了课外活动,求二班比三班多多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
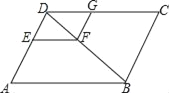
查看答案和解析>>
科目:初中数学 来源: 题型:
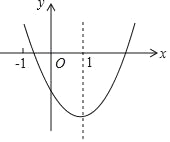
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com